Minitab 기술 지원 부서에서 근무할 당시 많은 고객들로부터 "Cpk와 Ppk의 차이가 뭐죠?"라는 질문을 받고는 했습니다. 이는 정말 좋은 질문입니다. 실제로 많은 실무자들이 Ppk를 무시하고 기본적으로 Cpk를 사용하고 있죠. 비유하자면 CpK는 두 명으로 구성된 아이돌 그룹의 인기 멤버이고, PpK는 존재감 없는 나머지 한 멤버라고나 할까요?
우선 합리적 부분군의 정의를 알아본 다음, CpK와 PpK의 차이점을 살펴보도록 하겠습니다.
합리적 부분군
합리적 부분군은 동일한 조건하에 도출된 측정치 집단입니다. 부분군은 공정의 스냅샷을 나타냅니다. 따라서 부분군을 구성하는 측정치는 비슷한 시점에 측정해야 합니다. 예를 들어 매시간 항목 5개를 표본으로 추출하면 부분군 크기는 5입니다.
공식, 정의 등
공정 능력 분석의 목표는 프로세스가 고객의 규격을 충족하는지 확인하는 것이며, 이때 평가에 Cpk와 Ppk 등의 공정 능력 통계를 사용합니다. 정규(분포) 공정 능력의 Cpk 및 Ppk 공식은 거의 동일하며,
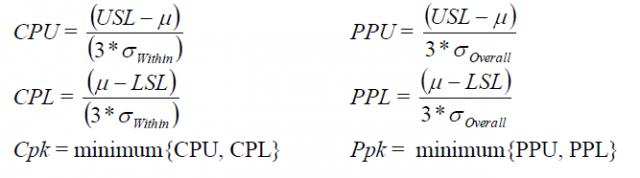
유일한 차이는 상위 통계와 하위 통계의 분모 뿐입니다. 즉, Cpk는 ‘내부’ 표준 편차를 사용하여 계산되는 반면, Ppk는 ‘전체’ 표준 편차를 사용하여 계산됩니다. 표준 편차에 관한 공식의 복잡한 세부 사항을 살펴볼 필요 없이 내부 표준 편차는 부분군 표준 편차의 평균으로, 전체 표준 편차는 모든 데이터의 변동을 나타내는 것으로 이해하면 됩니다. 즉, 다음과 같습니다.
Cpk:
- 부분군 내 변동만 설명
- D하위 그룹 간 이동 및 점진적 이동은 설명하지 않음
- 하위 그룹간에 변동이 없다는 가정하에 (시간의 경과 등에 따른) 공정의 규격 내에서 부품을 생산할 때의 잠재력을 나타내기 때문에 잠재적 기능 이라고도 함
Ppk:
- 측정한 모든 측정치의 전체 변동을 나타냄
- 이론적으로 부분군 내 변동과 부분군 간 이동 및 변동을 모두 포함
- 일반적인 하루 공정이 끝났을 때의 결과에 해당
CpK와 PpK의 차이에 관한 예시
10일간 매일 5회 측정을 실시하여 데이터 세트를 취합한 경우를 가정해 보겠습니다.
예시 1: 유사한 Cpk와 Ppk
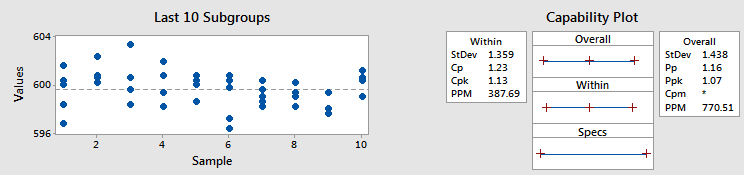
왼쪽 그래프가 나타내듯이 부분군 간 이동 및 변동은 부분군 내 변동에 비해 많지 않습니다. 즉, 내부 표준 편차와 전체 표준 편차가 비슷하므로 Cpk와 Ppk도 각각 1.13과 1.07로 비슷합니다.
예시 2: 다른 Cpk와 Ppk
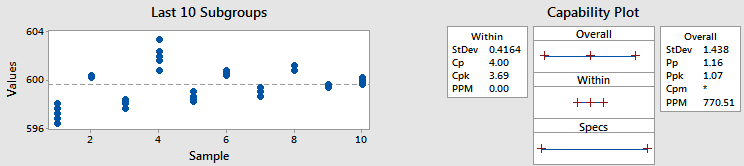
이 예에서는 동일한 데이터와 하위 그룹 크기를 사용하되, 데이터를 여러 하위 그룹으로 이동시켰습니다. 물론 실제로는 여러 하위 그룹으로 데이터를 이동시키면 안 되며, 이 예는 참고용일 뿐입니다.
같은 데이터를 사용했으므로 전체 표준 편차와 Ppk는 그대로입니다. 하지만 차이는 여기서부터입니다.
Cpk 통계를 보면 이전의 1.13에 비해 크게 개선된 3.69로 나타납니다. 부분군 그림에서 Cpk가 증가한 이유를 찾아볼 수 있습니다. 그래프의 각 부분군 내 점이 이전에 비해 훨씬 더 모여 있습니다. 앞서 표준 편차가 부분군 표준 편차의 평균을 나타낸다고 했는데요. 즉, 각 부분군 내 변동성이 더 작으면 표준 편차도 더 작아지므로 Cpk가 높아집니다.
Ppk 사용에 대한 고민
위 예에서 우리는 Cpk가 일부 정보만을 나타낸다는 사실을 확인할 수 있습니다. 따라서 공정 능력을 조사할 때는 Cpk와 Ppk를 모두 고려해야 하며, Cpk만 보고하고 Ppk를 아까 언급했던 아이돌 듀오 그룹의 이름 모를 멤버처럼 잊어서는 안 됩니다. 시간이 어느 정도 지나 공정이 안정화되고 변동이 감소하면 두 통계도 비슷해지게 됩니다.
(참고: 특히 부분군 크기가 1인 경우 Ppk가 Cpk 보다 클 수 있으며 이는 정상입니다. 이에 관한 설명은 다음에 하도록 하겠습니다.)



