by Matthew Barsalou, guest blogger
Programs such as the Minitab Statistical Software make hypothesis testing easier; but no program can think for the experimenter. Anybody performing a statistical hypothesis test must understand what p values mean in regards to their statistical results as well as potential limitations of statistical hypothesis testing.
A p value of 0.05 is frequently used during statistical hypothesis testing. This p value indicates that if there is no effect (or if the null hypothesis is true), you’d obtain the observed difference or more in 5% of studies due to random sampling error. However, performing multiple hypothesis tests with p > 0.05 increases the chance of a false positive.
This is well illustrated by the online comic XKCD, which depicted somebody stating that jelly beans cause acne.

Scientists investigated and found no link, so the person made the claim that it is only a certain color jelly bean that caused acne. The scientists then test 20 different colors of jelly beans with p > 0.05. Only the green jelly bean had a p value less than 0.05.
The comic ends with a newspaper reporting a link between green jelly beans and acne. The newspaper points out there is 95% confidence with only a 5% chance of coincidence. What is wrong with the conclusion?
We can determine the chance that there will be no false conclusions by using the binomial formula.
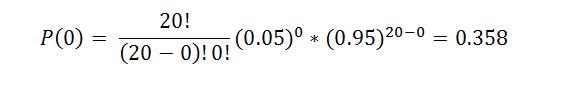
This means that we have a 35.8% chance of performing 20 hypothesis tests without getting a false positive (or, as statisticians refer to it, the family error rate) when using an alpha level of 0.05. We can also calculate the probability that we have at least one incorrect result due to random chance.
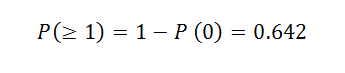
The chance that at least one result will be a false positive when performing 20 hypothesis tests using an alpha level of 0.05 is 64.2%.
So the press release in the XKCD comic may have been a bit premature.
Suppose I had 14 samples with a mean of 87.2 and I wanted to know if the mean is actually 85.2. I performed a One-Sample T-test using Minitab by going to Stat > Basic Statistics > 1 Sample t …. And I entered the summarized data. I checked the “perform hypothesis test box” and then selected “Options…” and used the default confidence level of 95.0. This corresponds to an alpha of 0.05.

I performed the test and the resulting p value was 0.049, which is close to but still below 0.05, so I can reject my null hypothesis. If I performed the test repeatedly, as in the XLCD example, I might have failed to reject the null hypothesis, because the 5% probability adds up with additional tests.
There are alternatives to statistical hypothesis testing; for example, Bayesian inference could be used in place of hypothesis testing with p values. But alternative methods have their own weaknesses, and they may be difficult for non-statisticians to use.
Instead of avoiding the use of hypothesis testing, we should account for its limitations. For example, by realizing that each repeat of the test increases the chance of a false positive, as illustrated by XKCD's jelly bean example.
We can’t simply retest over and over using the same p value and then conclude that we have results with statistical significance. For situations such as in the XKCD example, Simons, Nelson and Simonsohn recommend disclosing the total number of test that were performed. Had we known that 20 test had been performed with p > 0.05 we could realize that we may not need to avoid green jellybeans after all.
xkcd.com comic from http://xkcd.com/882/ used under Creative Commons Attribution- NonCommercial 2.5 License. http://xkcd.com/license.html



