Monte Carlo simulations have come a long way since they were initially applied in the 1940s when scientists working on the atomic bomb calculated the probabilities of one fissioning uranium atom causing a fission reaction in another. Today we’re going over how to create a Monte Carlo simulation for a known engineering formula and a DOE equation from Minitab.
Since those days when uranium was in short supply and there was little room for experimental trial and error, Monte Carlo simulations have always specialized in computing reliable probabilities from simulated data. Today, simulated data is routinely used in many scenarios, from materials engineering to medical device package sealing to steelmaking. It can be used in many situations where resources are limited or gathering real data would be too expensive or impractical. With Engage or Workspace’s Monte Carlo simulation tool, you have the ability to:
- Simulate the range of possible outcomes to aid in decision-making.
- Forecast financial results or estimate project timelines.
- Understand the variability in a process or system.
- Find problems within a process or system.
- Manage risk by understanding cost/benefit relationships.
The 4 Steps to Get Started for Any Monte Carlo Simulation
Depending on the number of factors involved, simulations can be very complex. But at a basic level, all Monte Carlo simulations have four simple steps:
1. Identify the Transfer Equation
To create a Monte Carlo simulation, you need a quantitative model of the business activity, plan, or process you wish to explore. The mathematical expression of your process is called the “transfer equation.” This may be a known engineering or business formula, or it may be based on a model created from a designed experiment (DOE) or regression analysis. Software like Minitab Engage and Minitab Workspace gives you the ability to create complex equations, even those with multiple responses that may be dependent on each other.
2. Define the Input Parameters
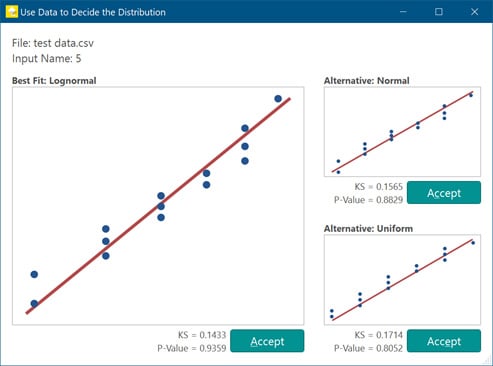
For each factor in your transfer equation, determine how its data are distributed. Some inputs may follow the normal distribution, while others follow a triangular or uniform distribution. You then need to determine distribution parameters for each input. For instance, you would need to specify the mean and standard deviation for inputs that follow a normal distribution. If you are unsure of what distribution your data follow, Engage and Workspace have a tool to help you decide.
3. Set up Simulation
For a valid simulation, you must create a very large, random data set for each input —something on the order of 100,000 instances. These random data points simulate the values that would be seen over a long period for each input. While it sounds like a lot of work, this is where Engage and Workspace shine. Once we submit the inputs and the model, everything here is taken care of.
4. Analyze Process Output
With the simulated data in place, you can use your transfer equation to calculate simulated outcomes. Running a large enough quantity of simulated input data through your model will give you a reliable indication of what the process will output over time, given the anticipated variation in the inputs.
The 4 Steps for Monte Carlo Using a Known Engineering Formula
A manufacturing company needs to evaluate the design of a proposed product: a small piston pump that must pump 12 ml of fluid per minute. You want to estimate the probable performance over thousands of pumps, given natural variation in piston diameter (D), stroke length (L), and strokes per minute (RPM). Ideally, the pump flow across thousands of pumps will have a standard deviation no greater than 0.2 ml.
1. Identify the Transfer Equation
The first step in doing a Monte Carlo simulation is to determine the transfer equation. In this case, you can simply use an established engineering formula that measures pump flow:
Flow (in ml) = π(D/2)2 ∗ L ∗ RPM
2. Define the Input Parameters
Now you must define the distribution and parameters of each input used in the transfer equation. The pump’s piston diameter and stroke length are known, but you must calculate the strokes-per-minute (RPM) needed to attain the desired 12 ml/minute flow rate. Volume pumped per stroke is given by this equation:
π(D/2)2 * L
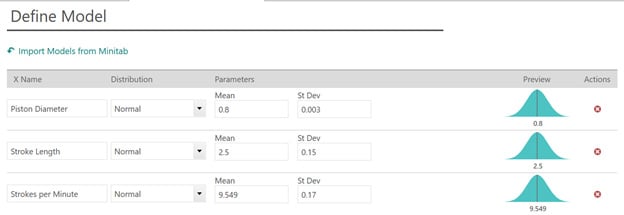
Given D = 0.8 and L = 2.5, each stroke displaces 1.256 ml. So to achieve a flow of 12 ml/minute the RPM is 9.549.
Based on the performance of other pumps your facility has manufactured, you can say that piston diameter is normally distributed with a mean of 0.8 cm and a standard deviation of 0.003 cm. Stroke length is normally distributed with a mean of 2.5 cm and a standard deviation of 0.15 cm. Finally, strokes per minute is normally distributed with a mean of 9.549 RPM and a standard deviation of 0.17 RPM.
3. Set up the Simulation in Engage or Workspace
Click the Insert tab from the top ribbon, and then choose Monte Carlo Simulation.

We made it easy – just give each variable a name, select a distribution from the drop-down menu and enter the parameters. We’ll stick with what we described above. If you are unsure of a distribution, you can select Use data to decide. This will prompt you to upload a .csv file of your data, and you will have a few options to choose from:
4. Simulate and Analyze Process Output
The next step is to give the equation. Here it’s as simple as giving your output a name (ours is Flow) and typing in the correct transfer equation which we identified above. You can also add upper and lower spec limits to see how your simulation compares.

Then, in the ribbon, choose how many simulations you want to run (100,000 is a good baseline) and click the button to run the simulation.
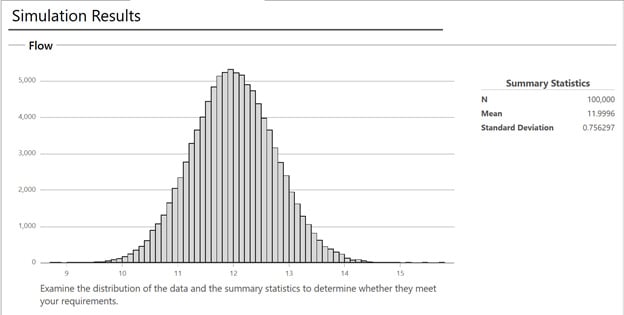
 For the random data generated to write this article, the mean flow rate is 11.996 based on 100,000 samples. On average, we are on target, but the smallest value was 8.7817 and the largest was 15.7057. That’s quite a range. The transmitted variation (of all components) results in a standard deviation of 0.756 ml, far exceeding the 0.2 ml target.
For the random data generated to write this article, the mean flow rate is 11.996 based on 100,000 samples. On average, we are on target, but the smallest value was 8.7817 and the largest was 15.7057. That’s quite a range. The transmitted variation (of all components) results in a standard deviation of 0.756 ml, far exceeding the 0.2 ml target.
It looks like this pump design exhibits too much variation and needs to be further refined before it goes into production. This is where we start to see the benefit of simulation. If we went right into production, we would have produced, most likely, too many rejected pumps. With Monte Carlo Simulation, we are able to figure all of this out without incurring the expense of manufacturing and testing thousands of prototypes or putting it into production prematurely.
Lest you wonder whether these simulated results hold up, try it yourself! Running different simulations will result in minor variations, but the end result — an unacceptable amount of variation in the flow rate — will be consistent every time. That’s the power of the Monte Carlo method.
One More Optional Step: Parameter Optimization
Learning the standard deviation is too high is extremely valuable, but where Engage and Workspace really stand out is their ability to help improve on the situation. That’s where Parameter Optimization comes in.
Let’s look at our first input, piston diameter. With an average of 0.8, most of our data will fall close to that value, or within one or two standard deviations. But what if it’s more efficient to our flow for the piston to have a smaller diameter? Parameter optimization helps us to answer that question.
To conduct parameter optimization, we need to specify a search range for each input. For this example, for simplicity, I designated a +/- 3 standard deviation range for the algorithm to search. Then, either Engage or Workspace will help us find the optimal settings for each input to achieve or goal, which in this case is to reduce the standard deviation. Selecting the appropriate range is important; make sure that the full range you input is feasible to run; it does no good to find an optimal solution that isn’t possible to replicate in production.
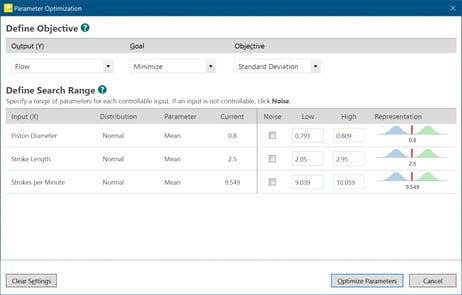
If you’ve used the Response Optimizer in Minitab Statistical Software, the idea is similar. Here are our results:
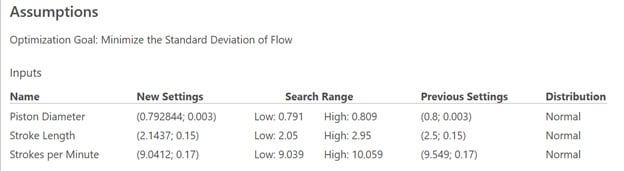
Based on this, if we want to reduce our standard deviation, we should reduce our Stroke Length and our Strokes per Minute. Our piston diameter can stay in a similar place. And remember the key to Monte Carlo simulation – we are able to find all of this out without building and single new prototype or conducting a new experiment.
Monte Carlo Using a Design of Experiments (DOE) Response Equation
What if you don’t know what equation to use, or you are trying to simulate the outcome of a unique process? This is where we can combine the designed experiment capabilities of Minitab Statistical Software with the simulation capabilities of Engage or Workspace.
An electronics manufacturer has assigned you to improve its electrocleaning operation, which prepares metal parts for electroplating. Electroplating lets manufacturers coat raw materials with a layer of a different metal to achieve desired characteristics. Plating will not adhere to a dirty surface, so the company has a continuous-flow electrocleaning system that connects to an automatic electroplating machine. A conveyer dips each part into a bath which sends voltage through the part, cleaning it. Inadequate cleaning results in a high Root Mean Square Average Roughness value, or RMS, and poor surface finish. Properly cleaned parts have a smooth surface and a low RMS.
To optimize the process, you can adjust two critical inputs: voltage (Vdc) and current density (ASF). For your electrocleaning method, the typical engineering limits for Vdc are 3 to 12 volts. Limits for current density are 10 to 150 amps per square foot (ASF).
1. Identify the Transfer Equation
You cannot use an established textbook formula for this process, but you can set up a Response Surface DOE in Minitab to determine the transfer equation. Response surface DOEs are often used to optimize the response by finding the best settings for a "vital few" controllable factors.
In this case, the response will be the surface quality of parts after they have been cleaned.
To create a response surface experiment in Minitab, choose Stat > DOE > Response Surface > Create Response Surface Design. Because we have two factors—voltage (Vdc) and current density (ASF)—we’ll select a two-factor central composite design, which has 13 runs.
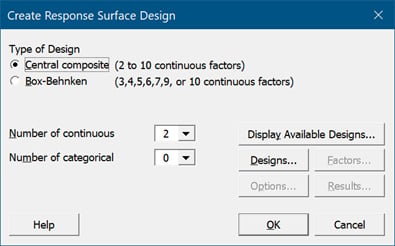
After Minitab creates your designed experiment, you need to perform your 13 experimental runs, collect the data, and record the surface roughness of the 13 finished parts. Minitab makes it easy to analyze the DOE results, reduce the model, and check assumptions using residual plots. Using the final model and Minitab’s response optimizer, you can find the optimum settings for your variables. In this case, you set volts to 7.74 and ASF to 77.8 to obtain a roughness value of 39.4.
The response surface DOE yields the following transfer equation for the Monte Carlo simulation:
Roughness = 957.8 − 189.4(Vdc) − 4.81(ASF) + 12.26(Vdc2) + 0.0309(ASF2)
2. Define the Input Parameters
Now you can set the parametric definitions for your Monte Carlo Simulation inputs and bring them over to Engage or Workspace.
Note that the standard deviations must be known or estimated based on existing process knowledge. This is true for all Monte Carlo inputs. Volts are normally distributed with a mean of 7.74 Vdc and a standard deviation of 0.14 Vdc. Amps per Square Foot (ASF) are normally distributed with a mean of 77.8 ASF and a standard deviation of 3 ASF.
3. Set up the Simulation in Engage or Workspace
This works exactly the same as Step 3. Click Insert > Monte Carlo Simulation from the ribbon, add your inputs and define their parameters, and then enter your model. In this case, if you have the latest version of Minitab you can right-click and hit Send to Engage or Send to Minitab Workspace. If not, you can manually copy it over from the Minitab output and paste it into the model field in Engage or Workspace.
4. Simulate and Analyze Process Output
The summary shows that even though the underlying inputs were normally distributed, the distribution of the RMS roughness is non-normal. The summary also shows that the transmitted variation of all components results in a standard deviation of 0.521, and process knowledge indicates this is a good process result. Based on a DOE with just 13 runs, we can determine the reality of what will be seen in the process. Again, since this is based on simulated data, your answers will be slightly different, but the general answers should be correct. If necessary, we can look at parameter optimization to tweak our answers and find an optimal solution.
This article is based on a presentation delivered by Paul Sheehy, Minitab technical training specialist, at the ASQ Lean Six Sigma Conference in February 2012.


