It’s safe to say that most people who use statistics are more familiar with parametric analyses than nonparametric analyses. Nonparametric tests are also called distribution-free tests because they don’t assume that your data follow a specific distribution.
You may have heard that you should use nonparametric tests when your data don’t meet the assumptions of the parametric test, especially the assumption about normally distributed data. That sounds like a nice and straightforward way to choose, but there are additional considerations.
In this post, I’ll help you determine when you should use a:
- Parametric analysis to test group means.
- Nonparametric analysis to test group medians.
In particular, I'll focus on an important reason to use nonparametric tests that I don’t think gets mentioned often enough!
Hypothesis Tests of the Mean and Median
Nonparametric tests are like a parallel universe to parametric tests. The table shows related pairs of hypothesis tests that Minitab Statistical Software offers.
| Parametric tests (means) |
Nonparametric tests (medians) |
| 1-sample t test |
1-sample Sign, 1-sample Wilcoxon |
| 2-sample t test |
Mann-Whitney test |
| One-Way ANOVA |
Kruskal-Wallis, Mood’s median test |
| Factorial DOE with one factor and one blocking variable |
Friedman test |
Reasons to Use Parametric Tests
Reason 1: Parametric tests can perform well with skewed and nonnormal distributions
This may be a surprise but parametric tests can perform well with continuous data that are nonnormal if you satisfy the sample size guidelines in the table below. These guidelines are based on simulation studies conducted by statisticians here at Minitab. To learn more about these studies, read our Technical Papers.
| Parametric analyses |
Sample size guidelines for nonnormal data |
| 1-sample t test |
Greater than 20 |
| 2-sample t test |
Each group should be greater than 15 |
| One-Way ANOVA |
|
Reason 2: Parametric tests can perform well when the spread of each group is different
While nonparametric tests don’t assume that your data follow a normal distribution, they do have other assumptions that can be hard to meet. For nonparametric tests that compare groups, a common assumption is that the data for all groups must have the same spread (dispersion). If your groups have a different spread, the nonparametric tests might not provide valid results.
On the other hand, if you use the 2-sample t test or One-Way ANOVA, you can simply go to the Options subdialog and uncheck Assume equal variances. Voilà, you’re good to go even when the groups have different spreads!
Reason 3: Statistical power
Parametric tests usually have more statistical power than nonparametric tests. Thus, you are more likely to detect a significant effect when one truly exists.
Reasons to Use Nonparametric Tests
Reason 1: Your area of study is better represented by the median
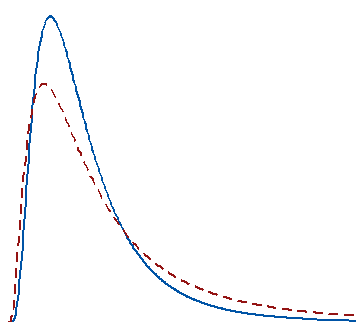 This is my favorite reason to use a nonparametric test and the one that isn’t mentioned often enough! The fact that you can perform a parametric test with nonnormal data doesn’t imply that the mean is the statistic that you want to test.
This is my favorite reason to use a nonparametric test and the one that isn’t mentioned often enough! The fact that you can perform a parametric test with nonnormal data doesn’t imply that the mean is the statistic that you want to test.
For example, the center of a skewed distribution, like income, can be better measured by the median where 50% are above the median and 50% are below. If you add a few billionaires to a sample, the mathematical mean increases greatly even though the income for the typical person doesn’t change.
When your distribution is skewed enough, the mean is strongly affected by changes far out in the distribution’s tail whereas the median continues to more closely reflect the center of the distribution. For these two distributions, a random sample of 100 from each distribution produces means that are significantly different, but medians that are not significantly different.
Two other blog posts illustrate this point well: The Non-parametric Economy: What Does Average Actually Mean?
Reason 2: You have a very small sample size
If you don’t meet the sample size guidelines for the parametric tests and you are not confident that you have normally distributed data, you should use a nonparametric test. When you have a really small sample, you might not even be able to ascertain the distribution of your data because the distribution tests will lack sufficient power to provide meaningful results.
In this scenario, you’re in a tough spot with no valid alternative. Nonparametric tests have less power to begin with and it’s a double whammy when you add a small sample size on top of that!
Reason 3: You have ordinal data, ranked data, or outliers that you can’t remove
Typical parametric tests can only assess continuous data and the results can be significantly affected by outliers. Conversely, some nonparametric tests can handle ordinal data, ranked data, and not be seriously affected by outliers. Be sure to check the assumptions for the nonparametric test because each one has its own data requirements.
If you have Likert data and want to compare two groups, read my post Best Way to Analyze Likert Item Data: Two Sample T-Test versus Mann-Whitney.
Closing Thoughts
It’s commonly thought that the need to choose between a parametric and nonparametric test occurs when your data fail to meet an assumption of the parametric test. This can be the case when you have both a small sample size and nonnormal data. However, other considerations often play a role because parametric tests can often handle nonnormal data. Conversely, nonparametric tests have strict assumptions that you can’t disregard.
The decision often depends on whether the mean or median more accurately represents the center of your data’s distribution.
- If the mean accurately represents the center of your distribution and your sample size is large enough, consider a parametric test because they are more powerful.
- If the median better represents the center of your distribution, consider the nonparametric test even when you have a large sample.
Finally, if you have a very small sample size, you might be stuck using a nonparametric test. Please, collect more data next time if it is at all possible! As you can see, the sample size guidelines aren’t really that large. Your chance of detecting a significant effect when one exists can be very small when you have both a small sample size and you need to use a less efficient nonparametric test!




