1年ほど前、統計における自由度を説明してほしいとのご要望を、ある読者から受けました。以来、慎重にこの件に取り組んでいます。まるで、安全にねじ伏せることができるかわからない獣のことを考えているかのように。
自由度を説明するのは、簡単ではありません。統計では、多くの異なる文脈で登場します。高度な文脈もあれば、複雑な文脈もあります。数学では、厳密には確率ベクトルの定義域の次元と定義されています。
でもそれには触れません。自由度は、一般的に、統計分析をするために理解すべき事柄ではないためです。調査統計家や統計理論を研究している人なら別ですが。
それでも、探究心を刺激されるものです。冒険心や好奇心が旺盛な人のために、統計におけるその意味の基本を要約いたします。
多様の自由
とりあえず、統計のことは忘れてください。あなたは帽子をかぶることが好きな、楽しいこと好きな人間だとしましょう。自由度が何かなんて、あなたは少しも気にしません。多様は人生のスパイスであり、多様な方がおもしろいと考えています。
でも残念ながら、制約があります。帽子を7個しか持っていないのです。でも1週間毎日違う帽子をかぶりたいと思っています。

1日目は、7個のうちのどれでも好きな帽子をかぶることができます。2日目は、残り6個から選べて、3日目は、残り5個から選べて、というように続いていきます。
6日目がやってくると、この週にまだかぶっていない2個からの選択になります。6日目の帽子を選んでしまうと、もう7日目の選択肢はありません。残っている1個をかぶるしかなくなります。7-1 = 6日間は「帽子」の自由がありました。多様な帽子をかぶる自由です!
これが統計における自由度の背景にある考え方です。自由度は、広義には、データの「観測値」の数(情報の件数)と定義され、統計パラメータを推定するときの多様の自由です。
自由度:1サンプルのt検定
次に、帽子ではなく、データ分析に首ったけだとしましょう。
値が10個あるデータセットがあるとします。何ら推定をしていなければ、各値は任意の数になりえますね?各値は完全な多様の自由です。
さて、1サンプルのt検定を用いて、10個の値のサンプルの母集団平均を検定するとします。制約が生じます。平均の推定です。この制約とは、具体的に何なのでしょうか?平均の定義により、次の関係が成り立つでしょう。データ内のすべての値の合計は、n x 平均に等しくなります。ここでは、nはデータセットの値の数です。
なので、データセットに値が10ある場合、その10の値の合計は平均 x 10に等しくなります。10の値の平均が3.5(任意の数を選択可能)の場合、この制約では10の値の合計が、10 x 3.5 = 35に等しくなる必要があります。
この制約があって、データセットの最初の値には、多様の自由があります。値が何であれ、10の値すべての合計が35になる可能性はあります。2番目の値にも多様の自由があります。どの値を選択しても、すべての値の合計が35になる可能性がまだあるためです。
実際、最初の9つの値は、次の2例を含め、何でもありえます。
34, -8.3, -37, -92, -1, 0, 1, -22, 99
0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9
ですが、10の値すべての合計が35、平均が3.5になるには、10番目の値に多様はありえません。特定の数になります。
9つの値が34、-8.3、-37、-92、-1、0、1、-22、99であれば、10番目の値は61.3
9つの値が0.1、0.2、0.3、0.4、0.5、0.6、0.7、0.8、0.9であれば、10番目の値は30.5
したがって、10 - 1 = 9の自由度になります。使用するサンプルサイズや平均値は関係なく、サンプルの最後の値に多様の自由はありません。結局、自由度n - 1になり、ここでは、nはサンプルサイズです。
別の言い方をすると、自由度の数 = 「観測値」の数 - 観測値間に必要な関係の数(パラメータ推定値の数)です。1サンプルt検定の場合、平均の推定に自由度1を使い、変動の推定に残りの自由度n - 1を使います。
次に、自由度を特定のt分布の定義に使います。t検定のp値とt値の計算に使用するものです。
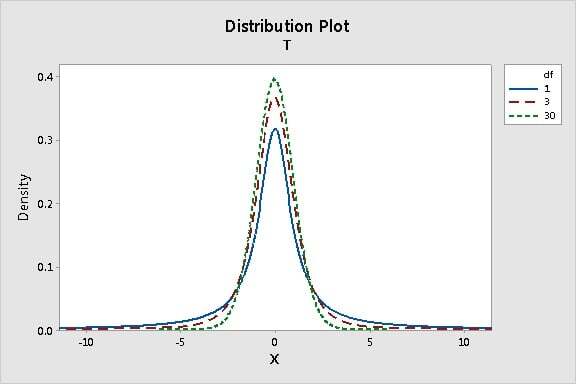
より小さい自由度(1サンプルt検定の場合はn - 1)に対応する小さな標本サイズ(n)の場合は、t分布の裾が広がります。これは、t分布が、小さい標本を分析するときにより慎重な検定結果を出すように特別に設計されているためです(醸造業界などで)。 標本サイズ(n)が大きくなると、自由度の数が増え、t分布は正規分布に近づきます。
自由度:独立性のカイ二乗検定
別の文脈を見てみましょう。独立性のカイ二乗検定は、2つのカテゴリ変数が依存しているかを判断するのに用います。この検定では、自由度は、行周辺合計と列周辺合計の制約があるため、多様性のあるカテゴリ変数の2次元の分割表内のセルの数です。ですから、この場合の各「観測値」は、セルの度数です。
最も単純な例を考えてみましょう。2 x 2表で、カテゴリごとに2つのカテゴリと2つの水準があります。
|
|
Category A |
Total |
|
| Category B |
? |
|
6 |
|
|
|
15 |
|
| Total |
10 |
11 |
21 |
行周辺合計と列周辺合計にどの値を使用するかは関係ありません。この値を設定すると、多様になるセル値は1つだけになります(ここでは左上のセルに「?」記号が表示されていますが、4つのセルのうちのどれか1つになります)。1つのセルに数値を入力すると、他のすべてのセルの数値は、行と列の合計で事前決定します。多様の自由はありません。したがって、独立性のカイ二乗検定には、2 x 2表の自由度が1つしかありません。
同様に、3 x 2表には2の自由度があります。特定の周辺合計のセットに対して多様になるのは2つのセルのみだからです。
|
|
Category A |
Total |
||
| Category B |
? |
? |
|
15 |
|
|
|
|
15 |
|
| Total |
10 |
11 |
9 |
30 |
さまざまなサイズの表を試してみると、最終的には一般的なパターンが見つかります。r行c列の表では、多様なセルの数値は (r-1)(c-1) です。これが、独立性のカイ二乗検定の自由度の公式です。
次に、自由度で、検定の独立性の評価に用いるカイ二乗分布を定義します。
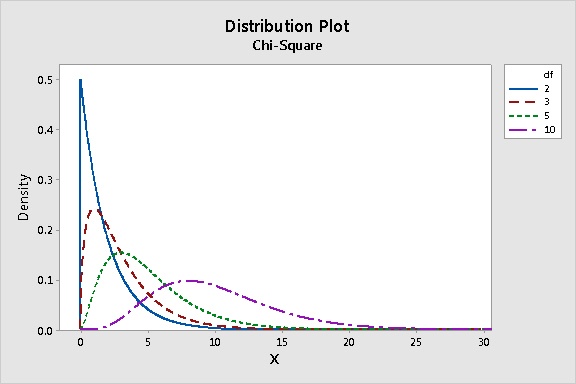
カイ二乗分布は正に歪んでいます。自由度が増すと、正規曲線に近づきます。
自由度:回帰
自由度は、回帰の文脈により深く関わっています。ここまで読んでくれた残り1人の読者(もしかしてお母さん?)を逃さないよう、これ以上の追求は控えます。
通常、自由度 = 観測値の数(または情報の件数) - パラメータ推定値の数だと述べました。回帰を実行すると、モデル内のすべての項のパラメータが推定され、各項が1つの自由度を使います。したがって、重回帰モデルに過剰な項を含めると、パラメータの変動性の推定に使える自由度が減ります。実際、データ量がモデル内の項の数に対して十分でない場合、自由度(degrees of freedom:DF)が誤差項に対してさえ十分でない可能性があり、p値またはF値は一切計算できません。次のような出力になります。
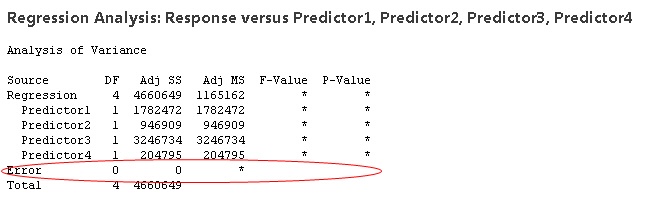
これが起こった場合は、より多くのデータを集めるか(自由度を増やすため)、モデルから項を削除する(必要な自由度の数を減らすため)必要があります。したがって、自由度は、確率ベクトルの定義域の冥府にあるのに、データ分析に具体的な影響を及ぼします。
フォローアップ
この記事には、統計における自由度の、基本的かつ非公式な内容を記載しています。自由度の概念的理解をさらに深めたい場合は、米国統計学会の初の女性会長だったコロンビアの教育准教授Dr. Helen Walkerが執筆したJournal of Educational Psychologyの論文をお読みください。別の一般的な良い参考資料として、S. PandyおよびC. L. Brightが執筆したSocial Work Research Vol 32, number 2, June 2008を、こちらから入手できます。



