회귀 분석을 통해 하나 이상의 예측 변수와 반응 변수의 통계적 관계를 설명하는 공식을 도출할 수 있습니다. Minitab Statistical Software를 사용하여 회귀 분석 모형을 적용하고 잔차 그림을 확인했다면 이제 결과를 해석해야 합니다. 이 게시물에서는 선형 회귀 분석 결과에 나타난 P값과 계수를 해석하는 방법을 설명합니다.
선형 회귀 분석의 P값을 해석하는 방법
T각 항의 P값은 계수가 0이라는(영향 없음) 귀무 가설을 검정합니다. P값이 낮으면(<0.05) 귀무 가설을 기각할 수 있습니다. 즉, P값이 낮은 예측 변수는 예측 변수 값의 변화가 반응 변수의 변화와 연관성이 있으므로 모델에 유의미한 요소로 작용할 수 있습니다.
반대로 더 큰 P값은(무의미함) 예측 변수의 변화가 반응의 변화와 연관성이 없다는 사실을 나타냅니다.
아래 결과에서 South와 North의 예측 변수는 P값이 모두 0.000이므로 유의합니다. 그러나 East의 P값(0.092)은 일반 알파 수준인 0.05보다 크므로 통계적으로 유의하지 않습니다.
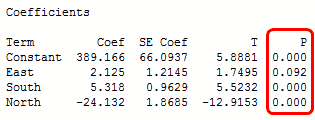
보통 계수 P값에 따라 회귀 분석 모형에 계속 포함할 항을 결정하게 됩니다. 따라서 위 모형에서는 East를 제거하는 것을 고려해야 합니다.
선형 관계의 회귀 계수를 해석하는 방법
회귀 계수는 모형의 다른 예측 변수를 유지하면서 예측 변수의 한 단위에 대한 반응 변수의 평균 변화를 나타냅니다. 이와 같은 회귀의 통계적 관리는 특정한 변수의 역할을 모형의 다른 변수로부터 분리하므로 중요합니다.
이러한 계수를 이해하는 좋은 방법은 계수를 경사로 생각하는 것입니다. 실제로 회귀 계수는 '기울기 계수'로 불리기도 합니다. 사람의 신장을 이용하여 체중을 모델링 한 아래의 적합선 그림 예시를 참조하세요. 우선 Minitab의 세션 창 결과를 보겠습니다.
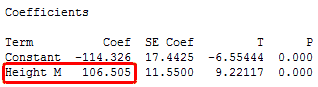
적합선 그림은 같은 회귀 결과를 그래픽으로 나타낸 것입니다.
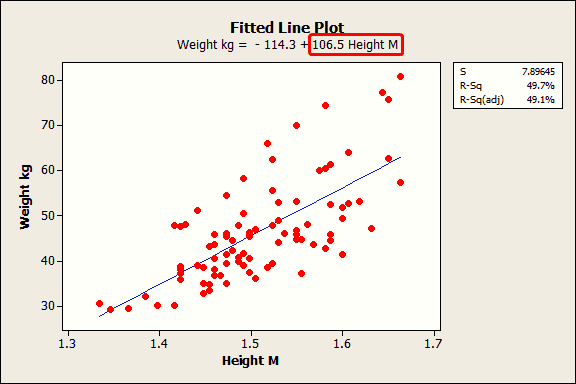
공식에 따르면, 신장(미터)의 계수는 106.5킬로그램입니다. 이 계수는 신장이 1미터 커질 때마다 체중이 평균 106.5킬로그램 증가할 것으로 예상된다는 사실을 나타냅니다.
파란색 적합선은 같은 정보를 그래픽으로 나타낸 것입니다. 신장 1미터 차이만큼 X축을 좌우로 움직이면 적합선이 106.5킬로그램만큼 상승하거나 하락합니다. 단, 이러한 신장 정보의 출처는 중학생 연령의 소녀들이며, 범위는 1.3~1.7m입니다. 따라서 이와 같은 관계는 해당 데이터 범위 내에서만 유효하므로, 이 예시에서는 X축을 1미터 단위로 이동할 수 없었습니다.
적합선이 평평하다면(기울기 계수 = 0) 선의 위쪽이나 아래쪽으로 이동해도 체중 기대 값이 변화하지 않습니다. 즉, P값이 낮으면 기울기가 0이 아니며, 따라서 예측 변수의 변화가 반응 변수의 변화와 연관되어 있음을 나타냅니다.
이는 적합선 그림에서 명확하게 확인할 수 있습니다. 단, 적합선 그림은 예측 변수 1개와 반응을 포함하는 단순 회귀 분석의 결과만 나타낼 수 있습니다. 이러한 개념은 다중 선형 회귀 분석에도 동일하게 적용되지만, 이 경우 추가되는 예측 변수의 결과를 나타낼 공간 차원이 더 필요합니다. 아쉽게도 오늘날의 기술로는 나타내기가 어려운 부분이죠.
곡선형 관계의 회귀 계수와 교호작용 항을 해석하는 방법
위 예시에서 신장은 선형 효과이며 기울기는 일정합니다. 이를 통해 효과가 적합선 전체에 걸쳐 일정하다는 사실을 알 수 있습니다. 그러나 모형에 다항식 또는 교호작용 항이 필요한 경우 해석이 좀 더 복잡해집니다.
이전에 알아보았듯이 다항식은 데이터의 곡면성을 모형화하며, 교호작용 항은 예측 변수 1개의 효과가 다른 예측 변수 값에 따라 달라짐을 나타냅니다.
다음 예에서는 곡면성 모형화에 2차(제곱)항을 필요로 하는 데이터 세트가 사용됩니다. 아래 결과에서 선형 항과 제곱항 모두의 P값이 유의하다는 사실을 확인할 수 있습니다.
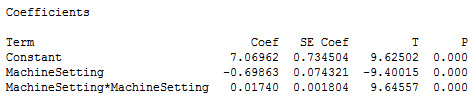
또한 잔차 그림(미표시)이 적합성을 나타내므로 해석을 진행할 수 있습니다. 그런데 이러한 계수를 어떻게 해석해야 할까요? 적합선 그림의 그래프로 나타내면 더 수월하게 해석할 수 있습니다.
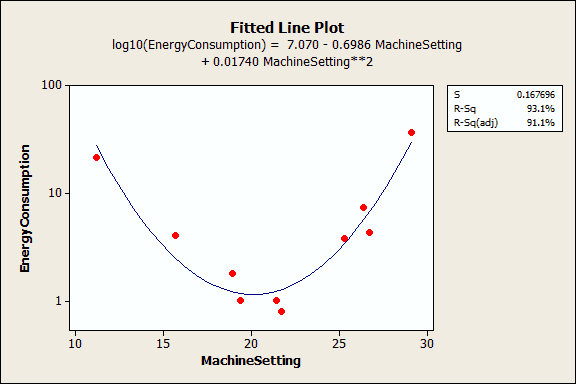
적합선의 시작 시점에 따라 기계 설정과 에너지 소비량의 관계가 달라지는 것을 확인할 수 있습니다. 예를 들어 기계 설정을 12에서 시작하여 1씩 높이면 에너지 소비량 감소를 기대할 수 있습니다. 그러나 기계 설정을 25에서 시작하여 1씩 높이면 에너지 소비량이 증가합니다. 또한 기계 설정이 20에 가까우면 에너지 소비량이 거의 변화하지 않습니다.
유의미한 다항이 있는 경우, 예측 변수 변화로 인한 효과가 해당 예측 변수의 값에 따라 달라지기 때문에 해석이 더 복잡해집니다. 마찬가지로 유의미한 교호작용 항은 예측 변수의 효과가 다른 예측 변수의 값에 따라 달라진다는 것을 나타냅니다.
이러한 유형의 항을 포함하는 회귀 모형을 해석할 때는 각별히 주의하시기 바랍니다. 주요 효과(선형 항)만 보고 분석하는 것은 불가능하니까요. 유감스럽게도 다중 회귀 분석을 수행하는 경우 적합선 그림을 이용하여 결과를 해석할 수 없습니다. 이 경우 주제 영역에 대한 지식이 더욱 빛을 발하겠죠!
예리한 분들은 제가 상수를 해석하는 방법을 소개하지 않았다는 사실을 눈치채셨을 텐데요. 이 내용은 다음 게시물에서 다루도록 하겠습니다!
잊지 말아야 할 사항:
회귀 분석에 대해 학습하는 분들은 제 회귀 튜토리얼을 참조하세요.




