약 1년 전에 한 독자가 통계의 자유도를 설명해 달라고 요청하셨습니다. 이후 저는 이 요청에 대해 매우 조심스러웠습니다.
자유도는 설명하기가 쉽지 않습니다. 자유도는 통계학에서 여러 상황에 등장하며, 일부는 복잡하고 어렵기도 합니다. 수학에서 자유도는 랜덤 벡터의 영역의 차원으로 정의됩니다.
이 내용은 더 파고들지 않도록 하겠습니다. 리서치 통계학자나 통계 이론 전공자가 아니라면 보통 자유도를 이해할 수 없어도 통계 분석을 수행할 수 있습니다.
그럼에도 불구하고 탐구심 많은 분들은 이 개념을 궁금해하곤 합니다. 따라서 모험과 호기심으로 가득한 분들을 위해 통계학에서 자유도의 기본적인 의미를 보여주는 몇 가지 예시를 준비했습니다.
변화의 자유
먼저 통계학은 잠시 잊고 여러분이 모자 쓰기를 좋아하며 재미를 추구하는 사람이라고 상상해보세요. 여러분은 자유도에 대해서는 알지도 못하고 알 생각도 없으며 다양성이 삶의 즐거움이라고 생각합니다.
하지만 불행히도 여러분에게 제약 사항이 있는데 바로 모자가 7개밖에 없다는 사실입니다. 여러분은 요일마다 다른 모자를 쓰고 싶습니다.
1일차에는 모자 7개 중 원하는 것을 쓸 수 있습니다. 2일차에는 남은 모자 6개 중에서 고를 수 있으며 3일차에는 모자 5개 중에서 고를 수 있습니다.
이런 식으로 6일차가 되면 여러분은 그 주에 아직 쓰지 않은 모자 2개 중 하나를 고를 수 있습니다. 하지만 6일차에 모자를 고르고 나면 7일차에는 더 이상 선택의 여지가 없이 마지막으로 남은 모자를 써야 합니다. 즉, 착용하는 모자가 달라지는 7-1 = 6일간의 '모자' 자유가 있었던 것이죠.
이것이 바로 통계학의 자유도 개념입니다. 대부분의 경우 자유도는 통계적 매개변수를 추정할 때 달라질 수 있는 데이터의 '관찰'(정보)의 수로 광범위하게 정의됩니다.
자유도: 1-표본 T-검정
그럼 여러분이 모자가 아니라 데이터 분석을 좋아한다고 가정해보겠습니다.
여러분에게 값이 10개인 데이터 세트가 있습니다. 추정하지 않는 경우 각각의 값은 임의의 숫자를 가질 수 있습니다. 즉, 각각의 값은 얼마든지 달라질 수 있습니다.
하지만 1-표본 t-검정을 통해 값이 10개인 표본으로 모집단 평균을 검정하려는 경우, 평균 추정이라는 제약이 생깁니다. 그렇다면 제약은 정확히 무엇일까요? 평균의 정의에 따르면 다음 관계가 성립해야 합니다. 데이터의 모든 값의 합계는 n x 평균과 같아야 합니다. 이 때 n은 데이터 세트의 값 수에 해당합니다.
즉, 데이터 세트에 값이 10개 있다면 10개 값의 합계가 평균 x 10과 동등해야 합니다. 10개 값의 평균이 3.5(어느 수든 상관없음)인 경우, 이 제약에 따라 10개 값의 합계가 10 x 3.5, 즉 35여야 합니다.
이러한 제약 조건을 전제로 데이터 세트의 첫째 값은 달라질 수 있습니다. 어느 값이든 10개 수의 합계는 여전히 35가 될 수 있으니까요. 두 번째 값 또한 달라질 수 있습니다. 어느 값을 선택하든 모든 값의 합계는 여전히 35가 될 수 있기 때문입니다.
실제로 다음 두 가지 예시처럼 9번째 값까지는 무엇이든 될 수 있습니다.
34, -8.3, -37, -92, -1, 0, 1, -22, 99
0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9
하지만 10개 값의 합이 35이고 평균이 3.5가 되려면 10번째 값은 달라질 수 없으며, 특정한 값이어야 합니다.
34, -8.3, -37, -92, -1, 0, 1, -22, 99 -----> 10번째 값은 61.3
0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9 ----> 10번째 값은 30.5
즉, 자유도는 10 - 1 = 9입니다. 사용하는 표본 크기 또는 평균값과는 상관없이 표본의 마지막 값은 자유로울 수 없으며, n - 1의 자유도가 도출됩니다. 이때 n은 표본 크기입니다.
이는 자유도 수가 '관찰' 수에서 관측치 사이에 필요한 관계의 수(즉, 모수 추정치의 수)를 뺀 것과 같다고도 표현할 수 있습니다. 1-표본 t-검정에서는 1의 자유도가 평균 추정에 사용되며, 나머지 n - 1의 자유도는 변동성을 추정합니다.
그런 다음 자유도는 t-검정의 p값과 t값 계산에 사용되는 t-분포를 정의합니다.
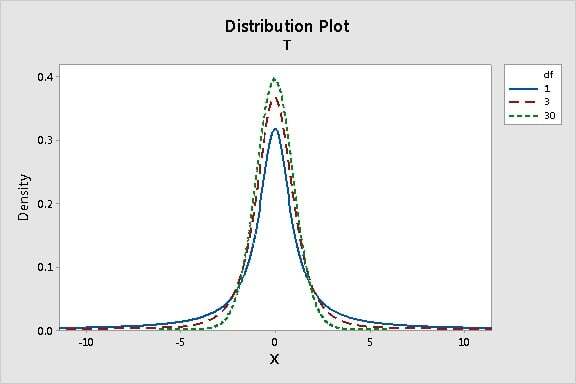
보시다시피 더 작은 자유도 (1-표본 t-검정의 경우 n -1) 에 해당하는 작은 표본 크기(n)의 경우 t-분포의 꼬리가 더 두껍습니다. 이는 보다 작은 표본(예: 양조 산업 등)을 분석하는 경우 t-분포가 더욱 보수적인 검정 결과를 제공하도록 설계되었기 때문입니다. 표본 크기(n)가 커질수록 자유도가 증가하고, t-분포는 정규 분포에 가까워집니다.
자유도: 카이-제곱 독립성 검정
또 다른 경우를 살펴보겠습니다. 카이-제곱 독립성 검정은 두 가지 범주형 변수가 종속적인지 파악하는 데 사용됩니다. 이 검정에서의 자유도는 행의 제약 조건과 열의 주변 합계를 고려했을 때 달라질 수 있는 범주형 변수의 이원표 셀 수에 해당합니다. 따라서 이 경우 각 '관찰'은 셀의 빈도입니다.
가장 간단한 예로 두 개의 범주와, 각 범주의 수준이 두개인 2 x 2 표를 가정해보겠습니다.
|
|
Category A |
Total |
|
| Category B |
? |
|
6 |
|
|
|
15 |
|
| Total |
10 |
11 |
21 |
행과 열의 주변 합계에 어떤 값을 사용하든 상관이 없습니다. 이 값들을 설정한 후에는 달라질 수 있는 셀 값이 하나 뿐입니다(이 경우 물음표로 표시되었으나, 4개 셀 중 아무 셀이든 될 수 있습니다). 한 셀에 숫자를 입력하면, 다른 모든 셀의 숫자는 행 및 열의 합계에 따라 미리 정해집니다. 즉, 이러한 셀들은 달라질 수 없습니다. 따라서 2 x 2 표의 카이-제곱 독립성 검정 결과, 자유도는 1입니다.
마찬가지로 3 x 2 표의 경우에도 정해진 주변 합계에 따르면 전체 셀 중 2개만이 달라질 수 있으므로 자유도는 2입니다.
|
|
Category A |
Total |
||
| Category B |
? |
? |
|
15 |
|
|
|
|
15 |
|
| Total |
10 |
11 |
9 |
30 |
여러 크기의 표로 실험하면 공통된 패턴을 확인할 수 있습니다. 즉, 행이 r개, 열이 c개 있는 표의 경우 달라질 수 있는 셀의 수는 (r-1) (c-1)입니다. 이것이 바로 카이-제곱 독립성 검정의 자유도 공식입니다!
그런 다음 자유도는 검정의 독립성을 평가하는 데 사용되는 카이-제곱 분포를 정의합니다.
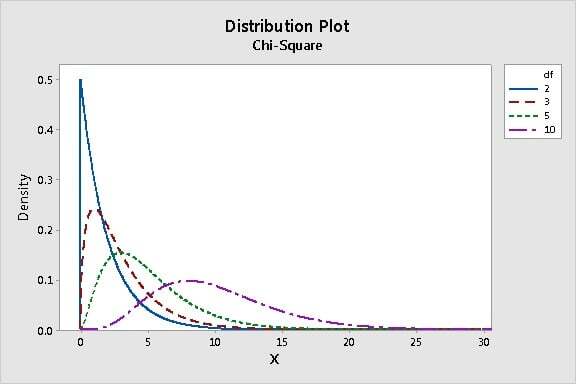
카이-제곱 분포는 양의 방향으로 치우쳐 있습니다. 자유도가 높아질수록 정규 곡선에 가까워집니다.
자유도: 회귀 분석
자유도는 회귀의 맥락에 더 깊이 연관되어 있습니다.
보통 자유도는 관찰(또는 정보)의 수에서 추정된 매개변수의 수를 뺀 것과 같습니다. 회귀를 수행할 때는 모형의 모든 항에 대해 모수가 추정되며, 각 항은 자유도를 소비합니다. 따라서 다중 회귀 모형의 과잉 조건을 포함하면 매개변수의 변동성을 추정하기 위해 사용할 수 있는 자유도가 낮아집니다. 실제로 데이터 양이 모형의 항 수만큼 충분하지 않다면 오차항에 대한 자유도(DF)가 부족하여 p값이나 F값을 계산하지 못하게 될 수도 있습니다. 이 경우 다음과 같은 결과가 도출됩니다.
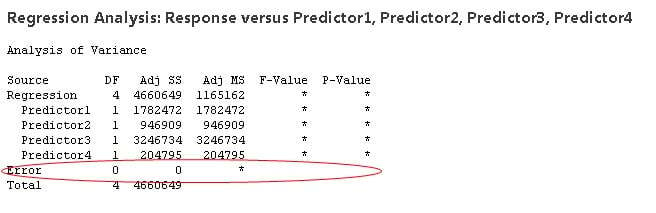
이러한 결과가 도출되면 더 많은 데이터를 수집하거나(자유도를 높이려면) 모형의 항을 삭제해야 합니다(필요한 자유도 수를 줄이려면). 즉, 자유도는 무작위 벡터 영역의 지하 세계에 존재함에도 불구하고 데이터 분석에 실질적인 영향을 줍니다.
추가 자료
이 게시물은 통계의 자유도에 대해 기본적이고 기초적인 사항을 소개했습니다. 자유도에 관한 이해를 더욱 높이고 싶으시다면 미국통계협회 최초의 여성 회장이었던 콜럼비아 교육대학교 부교수 Helen Walker 박사가 교육심리학 저널에 기고한 이 고전 논문을 참조하세요. 2008년 6월 2일에 발행된 Social Work Research 32권 2호에 수록된 Pandy, S. 및 Bright, C.L의 기고문도 참고하면 도움이 될 것입니다.



