Last week we began an experimental design trying to get at how to drive the golf ball the farthest off the tee by characterizing the process and defining the problem. The next step in our DOE problem-solving methodology is to design the data collection plan we’ll use to study the factors in the experiment.
We will construct a full factorial design, fractionate that design to half the number runs for each golfer, and then discuss the benefits of running our experiment as a factorial design.
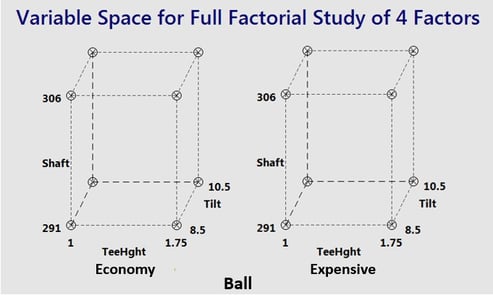
The four factors in our experiment and the low / high settings used in the study are:
- Club Face Tilt (Tilt) – Continuous Factor : 8.5 degrees & 10.5 degrees
- Ball Characteristics (Ball) – Categorical Factor : Economy & Expensive
- Club Shaft Flexibility (Shaft) – Continuous Factor : 291 & 306 vibration cycles per minute
- Tee Height (TeeHght) – Continuous Factor : 1 inch & 1 3/4 inch
To develop a full understanding of the effects of 2 – 5 factors on your response variables, a full factorial experiment requiring 2k runs ( k = of factors) is commonly used. Many industrial factorial designs study 2 to 5 factors in 4 to 16 runs (25-1 runs, the half fraction, is the best choice for studying 5 factors) because 4 to 16 runs is not unreasonable in most situations. The data collection plan for a full factorial consists of all combinations of the high and low setting for each of the factors. A cube plot, like the one for our golf experiment shown below, is a good way to display the design space the experiment will cover.
There are a number of good reasons for choosing this data collection plan over other possible designs. The details are discussed in many excellent texts. Here are my top five.
1. Factorial and fractional factorial designs are more cost-efficient.
Factorial and fractional factorial designs provide the most run efficient (economical) data collection plan to learn the relationship between your response variables and predictor variables. They achieve this efficiency by assuming that each effect on the response is linear and therefore can be estimated by studying only two levels of each predictor variable.
After all, it only takes two points to establish a line.
2. Factorial designs estimate the interactions of each input variable with every other input variable.
Often the effect of one variable on your response is dependent on the level or setting of another variable. The effectiveness of a college quarterback is a good analogy. A good quarterback can have good skills on his own. However, a great quarterback will achieve outstanding results only if he and his wide receiver have synergy. As a combination, the results of the pair can exceed the skill level of each individual player. This is an example of a synergistic interaction.
Complex industrial processes commonly have interactions, both synergistic and antagonistic, occurring between input variables. We cannot fully quantify the effects of input variables on our responses unless we have identified all active interactions in addition to the main effects of each variable. Factorial experiments are specifically designed to estimate all possible interactions.
3. Factorial designs are orthogonal.
We analyze our final experiment results using least squares regression to fit a linear model for the response as a function of the main effects and two-way interactions of each of the input variables. A key concern in least squares regression arises if the settings of the input variables or their interactions are correlated with each other. If this correlation occurs, the effect of one variable may be masked or confounded with another variable or interaction making it difficult to determine which variables actually cause the change in the response. When analyzing historical or observational data, there is no control over which variable settings are correlated with other input variable settings and this casts a doubt on the conclusiveness of the results. Orthogonal experimental designs have zero correlation between any variable or interaction effects specifically to avoid this problem. Therefore, our regression results for each effect are independent of all other effects and the results are clear and conclusive.
4. Factorial designs encourage a comprehensive approach to problem-solving.
First, intuition leads many researchers to reduce the list of possible input variables before the experiment in order to simplify the experiment execution and analysis. This intuition is wrong. The power of an experiment to determine the effect of an input variable on the response is reduced to zero the minute that variable is removed from the study (in the name of simplicity). Through the use of fractional factorial designs and experience in DOE, you quickly learn that it is just as easy to run a 7 factor experiment as a 3 factor experiment, while being much more effective.
Second, factorial experiments study each variable’s effect over a range of settings of the other variables. Therefore, our results apply to the full scope of all the process parameter settings rather than just specific settings of the other variables. Our results are more widely applicable to all conditions than the results from studying one variable at a time.
5. Two-level factorial designs provide an excellent foundation for a variety of follow-up experiments.
This will lead to the solution to your process problem. A fold-over of your initial fractional factorial can be used to complement an initial lower resolution experiment, providing a complete understanding of all your input variable effects. Augmenting your original design with axial points results in a response surface design to optimize your response with greater precision. The initial factorial design can provide a path of steepest ascent / descent to move out of your current design space into one with even better response values. Finally, and perhaps most commonly, a second factorial design with fewer variables and a smaller design space can be created to better understand the highest potential region for your response within the original design space.
I hope this short discussion has convinced you that any researcher in academics or industry will be well rewarded for the time spent learning to design, execute, analyze, and communicate the results from factorial experiments. The earlier in your career you learn these skills, the … well, you know the rest.
For these reasons, we can be quite confident about our selection of a full factorial data collection to study the 4 variables for our golf experiment. Each golfer will be responsible for executing only one half of the runs, called a half fraction, of the full factorial. Even so, the results for each golfer can be analyzed independently as a complete experiment.
In my next post, I’ll answer the question: How do we calculate the number of replicates needed for each set of run conditions from each golfer so that our results have a high enough power that we can be confident in our conclusions? Many thanks to Toftrees Golf Resort and Tussey Mountain for use of their facilities to conduct our golf experiment.
Catch Up with the other Golf DOE Posts:
Part 1: A (Golf) Course in Design of Experiments
Part 3: Mulligan? How Many Runs Do You Need to Produce a Complete Data Set?
Part 4: ANCOVA and Blocking: 2 Vital Parts to DOE
Part 5: Concluding Our Golf DOE: Time to Quantify, Understand and Optimize


