In my post Assessing Variability for Quality Improvement, I showed how measuring variability is as important as measuring the mean for a product or service in a quality improvement initiative. The mean, by itself, often tells an incomplete story. Additionally, quality management veterans know that controlling the variability is often more difficult than controlling the mean. If you want to change the mean, it often entails adjusting a manufacturing setting or target. However, reducing variability often requires new technology or new procedures.
For example, in the image above, it’s generally easier to re-center the tightly clustered measurements on a target than it is to reduce the spread of the dots that are centered.
This rule of thumb applied to a research project that I was involved in.
The Scenario
The study looked at bone density in teen girls. Specifically, we wanted to determine whether jumping from 24-inch steps, 30 times, every other school day would increase their bone density compared to the control group. For the jumping intervention, we wanted the subjects to experience an impact of 6 times their body weight (BW) for each jump.
I conducted a pilot study to quantify the impacts by having each subject jump 5 times onto a force plate. After data analysis, I found that the average impact -- the mean -- across all subjects was 6.13 BWs, which sounds great. However, I also found that variability was too high with a standard deviation of 1.08 body weights. While the overall mean exceeded our target, nearly half the subjects had means that were below 6 BWs. Subject means ranged from 4.7 to 8.4.
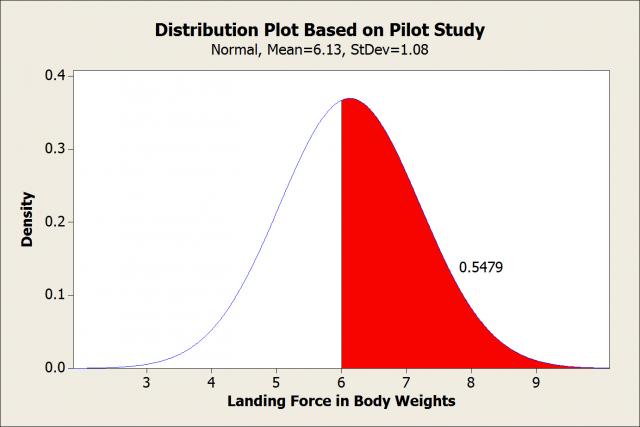
Minitab's probability distribution plot shows the distribution of landing forces using the distribution, mean, and standard deviation estimates from the pilot study. The shaded area indicates that we can expect that only 55% of the subjects will average over 6 body weights, our target.
Why Reducing Variability is Important
If you don’t know the nature of your process inputs, the outcomes may be unpredictable. Landing impacts were the key treatment for our study. High variability here would be equivalent to studying the effects of a drug but giving each subject wildly different, unknown doses! Or building a bridge, but being unsure of the strength of the material!
Peak Impact Background Information
While the subjects jumped from a fixed height, the magnitude of the peak impact depends upon how much the jumpers flex their knees. Theoretically, if jumpers did not flex their knees at all, they could exceed 50 BWs and injure their knees! The fact that the impacts were down in the 4-8 BW range was due to the subjects bending their knees on landing.
We found that the amount of knee bending was very sensitive to external factors. You can read here about how I found that subjects who did not wear shoes in previous jumps had significantly reduced impacts in later jumps, even when wearing shoes. Also, I compared impacts for jumping on a mat versus no mat. Surprisingly, the peak impacts on the mat were actually slightly higher! We hypothesized that seeing the mat subconsciously suggested to the subjects that they didn’t need to cushion the impact through knee flexing as much.
Digging Deeper
I dug a bit deeper and used an Xbar-S control chart in a slightly unconventional manner. Each subgroup represents a subject. Consequently, each plotted point represents the mean and standard deviation of each subject’s 5 trials (except for subject 2, who had a missing value).
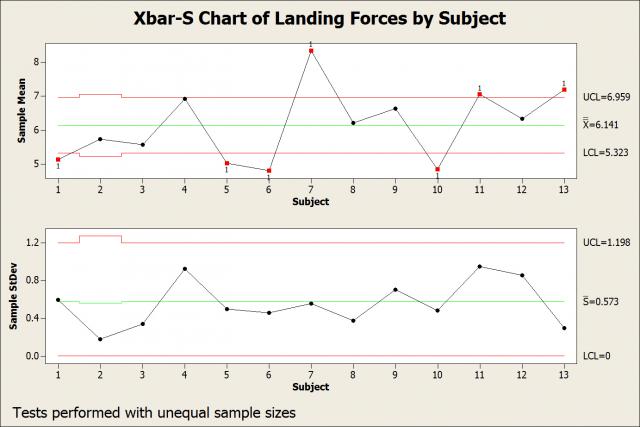
The in-control S chart shows that each subject has a consistent landing style that produces impacts of a consistent magnitude. However, the out-of-control Xbar chart indicates that different subjects have very different means. Collectively, the chart shows that some subjects are consistently hard landers while others are consistently soft landers. The control chart suggests that the variability is not inherent in the process (common cause variation) but rather assignable to differences between subjects (special cause variation). This begs the question, can we train the subjects to land a certain way?
Reducing the Variability
If we simply wanted to increase the mean we could’ve easily made the steps higher. In the range that I tested (8, 16, and 24 inches), I found that adding 8 inches to the jumping height increases the impact by an average of 2 BWs. However, our mean was acceptable and we needed to control the variability between subjects, which entailed a bit more of an involved, ongoing process change.
We decided that we needed to train the subjects how to land. For the training, we created a short video which demonstrated the proper way to land. The subjects were shown this video several times a school year. Additionally, the nurse for the research study observed all of the jumping sessions, looked for deep knee bends, and corrected each subject as needed. This ongoing training and corrective action reduced the variability enough so that the impacts were consistently greater than 6 BWs.
This simple jumping example illustrates how reducing the variability is often more difficult than improving the mean, which would’ve just required higher steps. Next time, I'll highlight another aspect of too much variation: how it can obscure significance in statistics.


