In statistics, there are things you need to do so you can trust your results. For example, you should check the sample size, the assumptions of the analysis, and so on. In regression analysis, I always urge people to check their residual plots.
In this blog post, I present one more thing you should do so you can trust your regression results in certain circumstances—standardize the continuous predictor variables. Before you groan about having one more thing to do, let me assure you that it’s both very easy and very important. In fact, standardizing the variables can actually reveal statistically significant findings that you might otherwise miss!
When and Why to Standardize the Variables
You should standardize the variables when your regression model contains polynomial terms or interaction terms. While these types of terms can provide extremely important information about the relationship between the response and predictor variables, they also produce excessive amounts of multicollinearity.
Multicollinearity is a problem because it can hide statistically significant terms, cause the coefficients to switch signs, and make it more difficult to specify the correct model.
Your regression model almost certainly has an excessive amount of multicollinearity if it contains polynomial or interaction terms. Fortunately, standardizing the predictors is an easy way to reduce multicollinearity and the associated problems that are caused by these higher-order terms. If you don’t standardize the variables when your model contains these types of terms, you are at risk of both missing statistically significant results and producing misleading results.
How to Standardize the Variables
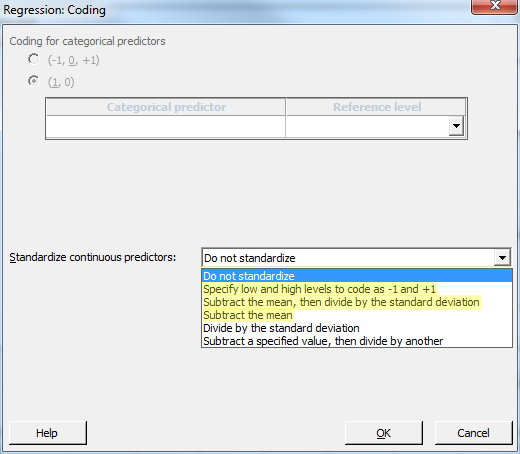 Many people are not familiar with the standardization process, but in Minitab Statistical Software it’s as easy as choosing an option and then proceeding along normally. All you need to do is click the Coding button in the main dialog and choose an option from Standardize continuous predictors.
Many people are not familiar with the standardization process, but in Minitab Statistical Software it’s as easy as choosing an option and then proceeding along normally. All you need to do is click the Coding button in the main dialog and choose an option from Standardize continuous predictors.
To reduce multicollinearity caused by higher-order terms, choose an option that includes Subtract the mean or use Specify low and high levels to code as -1 and +1.
These two methods reduce the amount of multicollinearity. In my experience, both methods produce equivalent results. However, it’s easy enough to try both methods and compare the results. The -1 to +1 coding scheme is the method that DOE models use. I tend to use Subtract the mean because it’s a more intuitive process. Subtracting the mean is also known as centering the variables.
One caution: the other two standardization methods won't reduce the multicollinearity.
How to Interpret the Results When You Standardize the Variables
Conveniently, you can usually interpret the regression coefficients in the normal manner even though you have standardized the variables. Minitab uses the coded values to fit the model, but it converts the coded coefficient back into the uncoded (or natural) values —as long as you fit a hierarchical model. Consequently, this feature is easy to use and the results are easy to interpret.
I’ll walk you through an example to show you the benefits, how to identify problems, and how to determine whether they have been resolved. This example comes from a previous post where I show how to compare regression slopes. You can get the data here.
In the first model, the response variable is Output and the predictors are Input, Condition, and the interaction term, Input*Condition.
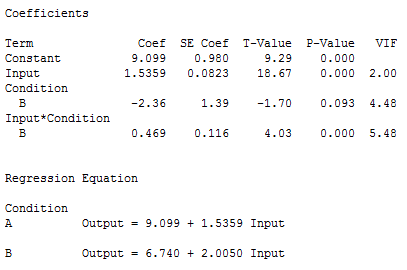
For the results above, if you use a significance level of 0.05, Input and Input*Condition are statistically significant, but Condition is not significant. However, VIFs greater than 5 suggest problematic levels of multicollinearity, and the VIFs for Condition and the interaction term are right around 5.
I’ll refit the model with the same terms but I’ll standardize the continuous predictors using the Subtract the mean method.
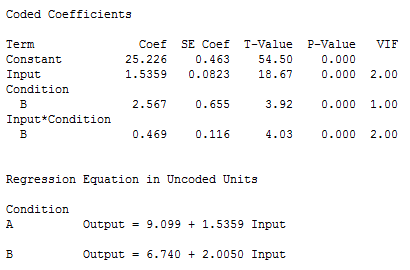
These results show that multicollinearity has been reduced because all of the VIFs are less than 5. Importantly, Condition is now statistically significant. Multicollinearity was obscuring the significance in the first model! The coefficients table shows the coded coefficients, but Minitab has converted them back into uncoded coefficients in the regression equation. You interpret these uncoded values in the normal manner.
This example shows the benefits of standardizing the variables when your regression model contains polynomial terms and interaction terms. You should always standardize when your model contains these types of terms. It is very easy to do and you’ll have more confidence that you’re not missing something important!
For more information, see my blog post What Are the Effects of Multicollinearity and When Can I Ignore Them? That post provides a more detailed explanation about the effects of multicollinearity and a different example of how standardizing the variables can reveal significant findings, and even a changing coefficient sign, that would have otherwise remained hidden.
If you're learning about regression, read my regression tutorial!



