Minitab Statistical Software offers three tests for Normality: Anderson-Darling (AD), Ryan-Joiner (RJ), and Kolmogorov-Smirnov (KS). The AD test is the default, but is it the best test at detecting Non-Normality? Let's compare the ability of each of these normality tests to detect non-normal data under three different scenarios. We'll use simulated data for each, but they reflect common situations you're likely to encounter if you're analyzing data for quality improvement.
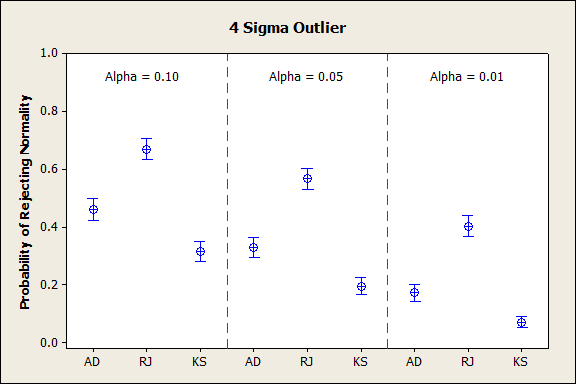
Scenario 1 – The manufacturing process produces large outliers from time to time. In this simulation, 29 values are simulated from a Normal (mean = 0, standard deviation = 1), and 1 value is simulated from a Normal (mean = 0, standard deviation = 4).
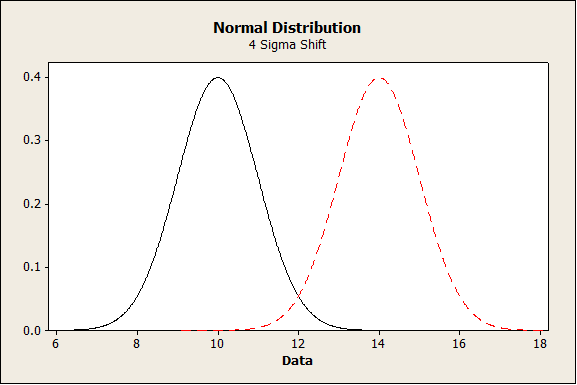
Scenario 2 – The manufacturing process has a process change that results in a shift in the distribution. This creates a bimodal distribution with a 4 sigma difference between the means and a sample size of 30. The graph below shows a 4 sigma difference in means between two normal distributions.
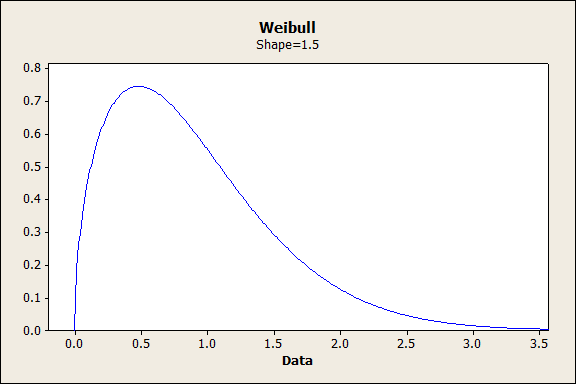
Scenario 3 – The measurements naturally follow a Non-normal distribution, as we'd typically see with time-to-failure data or strength measurements. For this scenario, 30 values are simulated from a Weibull (a = 1, b = 1.5) distribution.
I should note that the three scenarios evaluated in this blog are not designed to assess the validity of the Normality assumption for tests that benefit from the Central Limit Theorem, such as such as 1-sample, 2-sample, and paired t-tests. Our focus here is detecting Non-Normality when using a distribution to estimate the probability of manufacturing defective (out-of-spec) unit.
In scenario 1, the Ryan-Joiner test was a clear winner. The simulation results are below.
In scenario 2, the Anderson-Darling test was the best. The simulation results are below.

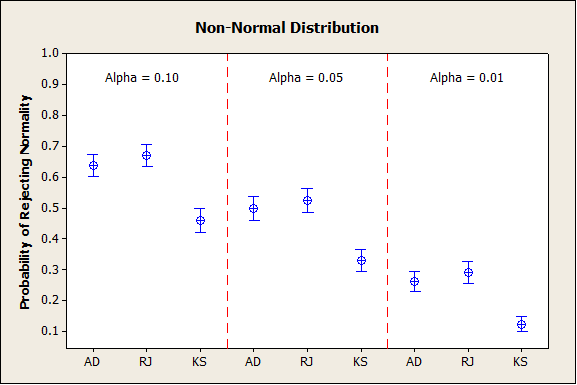
In scenario 3, there was not much difference between the AD and RJ test. Both were more effective at detecting Non-Normality than the Kolmogorov-Smirnov test. The simulation results are below.
In summary, the Anderson-Darling test was never the worst test, but it was not nearly as effective as the RJ test at detecting a 4-sigma outlier. If you're analyzing data from a manufacturing process tends to produce individual outliers, the Ryan-Joiner test is the most appropriate.
The RJ test performed very well in two of the scenarios, but was poor at detecting Non-Normality when there was a shift in the data. If you're analyzing data from a manufacturing process that tends to shift due to unexpected changes, the AD test is the most appropriate.
The KS test did not perform well in any of the scenarios.
In a future post, I'll discuss using an Individuals Control Chart to detect special-cause variation. (If special cause variation is detected, then Normality should not be assumed.) I'll also discuss how well these three tests do at not rejecting Normality when data are simulated from a Normal distribution and there is some degree of rounding applied to the data.



