In Part 1 of Gauging Gage, I looked at how adequate a sampling of 10 parts is for a Gage R&R Study and providing some advice based on the results.
Now I want to turn my attention to the other two factors in the standard Gage experiment: 3 operators and 2 replicates. Specifically, what if instead of increasing the number of parts in the experiment (my previous post demonstrated you would need an unfeasible increase in parts), you increased the number of operators or number of replicates?
In this study, we are only interested in the effect on our estimate of overall Gage variation. Obviously, increasing operators would give you a better estimate of of the operator term and reproducibility, and increasing replicates would get you a better estimate of repeatability. But I want to look at the overall impact on your assessment of the measurement system.
Operators
First we will look at operators. Using the same simulation engine I described in Part 1, this time I did two different simulations. In one, I increased the number of operators to 4 and continued using 10 parts and 2 replicates (for a total of 80 runs); in the other, I increased to 4 operators and still used 2 replicates, but decreased the number of parts to 8 to get back close to the original experiment size (64 runs compared to the original 60).
Here is a comparison of the standard experiment and each scenario laid out here:
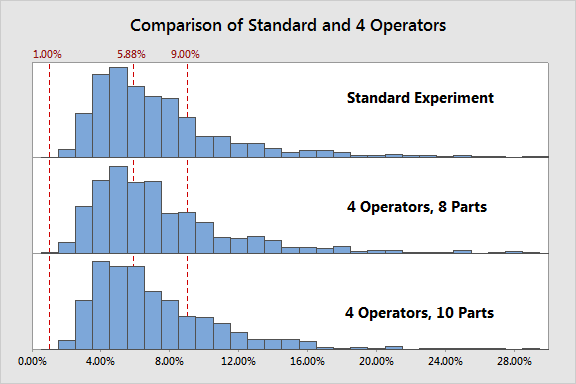
It may not be obvious in the graph, but increasing to 4 operators while decreasing to 8 parts actually increased the variation in %Contribution seen...so despite requiring 4 more runs this is the poorer choice. And the experiment that involved 4 operators but maintained 10 parts (a total of 80 runs) showed no significant improvement over the standard study.
Replicates
Now let's look at replicates in the same manner we looked at parts. In one run of simulations we will increase replicates to 3 while continuing to use 10 parts and 3 operators (90 runs), and in another we will increase replicates to 3 and operators to 3, but reduce parts to 7 to compensate (63 runs).
Again we compare the standard experiment to each of these scenarios:
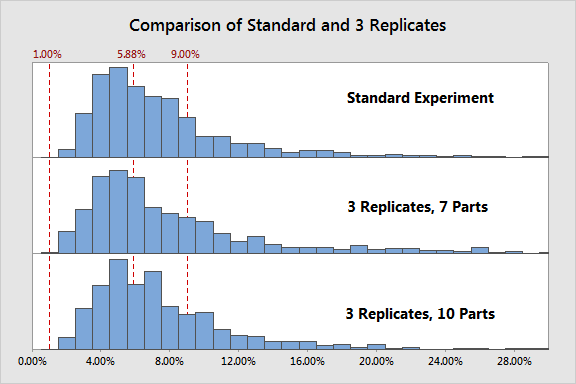

Here we see the same pattern as with operators. Increasing to 3 replicates while compensating by reducing to 7 parts (for a total of 63 runs) significantly increases the variation in %Contribution seen. And increasing to 3 replicates while maintaining 10 parts shows no improvement.
Conclusions about Operators and Replicates in Gage Studies
As stated above, we're only looking at the effect of these changes to the overall estimate of measurement system error. So while increasing to 4 operators or 3 replicates either showed no improvement in our ability to estimate %Contribution or actually made it worse, you may have a situation where you are willing to sacrifice that in order to get more accurate estimates of the individual components of measurement error. In that case, one of these designs might actually be a better choice.
For most situations, however, if you're able to collect more data, then increasing the number of parts used remains your best choice.
But how do we select those parts? I'll talk about that in my next post!



