*Algunos enlaces relacionados pueden contener información en otros idiomas
Después de ajustar un modelo lineal usando el análisis de regresión, el análisis ANOVA o el diseño de experimentos (DOE), se debe determinar qué tan bien se ajusta el modelo a los datos. A modo de ayuda, Minitab Statistical Software presenta una variedad de estadísticos de bondad de ajuste. En esta publicación, exploraremos el estadístico R-cuadrado (R2 ), algunas de sus limitaciones, y descubriremos varias sorpresas sobre la marcha. Por ejemplo, los valores bajos del R-cuadrado no siempre son malos y los valores altos del R-cuadrado no siempre son buenos.
¿Qué es la Bondad de Ajuste en el caso de un modelo lineal?
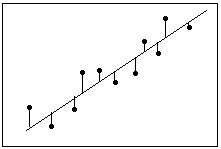Definición: Residuo = Valor observado - valor ajustadoLa regresión lineal calcula una ecuación que minimiza la distancia entre la línea ajustada y todos los puntos de los datos. Técnicamente, la regresión de mínimos cuadrados ordinarios (MCO) minimiza la suma de los residuos al cuadrado.
En general, un modelo se ajusta bien a los datos si las diferencias entre los valores observados y los valores de predicción del modelo son pequeñas y no presentan sesgo.
Antes de examinar las medidas estadísticas de bondad de ajuste, se recomienda revisar las gráficas de residuos. Las gráficas de residuos pueden revelar patrones no deseados de residuos que indican sesgo en los resultados de una manera más efectiva que los números. Cuando las gráficas de residuos pasan la revisión, se puede confiar en los resultados numéricos y verificar los bondad de ajuste estadística.
¿Qué es el R-cuadrado?
El R-cuadrado es una medida estadística de qué tan cerca están los datos de la línea de regresión ajustada. También se conoce como coeficiente de determinación, o coeficiente de determinación múltiple si se trata de regresión múltiple.
La definición de R-cuadrado es bastante sencilla: es el porcentaje de la variación en la variable de respuesta que es explicado por un modelo lineal. Es decir:
R-cuadrado = Variación explicada / variación total
El R-cuadrado siempre está entre 0 y 100%:
- 0% indica que el modelo no explica ninguna porción de la variabilidad de los datos de respuesta en torno a su media.
- 100% indica que el modelo explica toda la variabilidad de los datos de respuesta en torno a su media.
En general, cuanto mayor es el R-cuadrado, mejor se ajusta el modelo a los datos. Sin embargo, hay condiciones importantes con respecto a esta pauta de las que hablaré más adelante.
Representación Gráfica del R-cuadrado
Representar gráficamente los valores ajustados en función de los valores observados ilustra diferentes valores del R-cuadrado para los modelos de regresión.
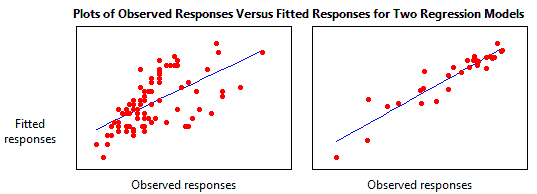
El modelo de regresión de la izquierda explica el 38% de la varianza, mientras que el de la derecha explica el 87,4%. Cuanto mayor sea la varianza explicada por el modelo de regresión, más cerca estarán los puntos de los datos de la línea de regresión ajustada. En teoría, si un modelo pudiera explicar el 100% de la varianza, los valores ajustados siempre serían iguales a los valores observados y, por lo tanto, todos los puntos de los datos estarían sobre la línea de regresión ajustada.
Limitaciones Claves del R-cuadrado
El R-cuadrado no puede determinar si las estimaciones y predicciones de los coeficientes están sesgadas, y es por eso que se deben examinar las gráficas de residuos.
El R-cuadrado no indica si un modelo de regresión es adecuado. Se puede tener un valor bajo del R-cuadrado para un modelo adecuado o un valor alto del R-cuadrado para un modelo que no se ajusta a los datos.
El R-cuadrado que se indica en la salida es una estimación sesgada del R-cuadrado de la población.
¿Son Inherentemente Malos los Valores Bajos del R-cuadrado?
¡No! Hay dos razones principales por las que los valores bajos del R-cuadrado podrían considerarse adecuados.
En algunos campos, se espera completamente que los valores del R-cuadrado sean bajos. Por ejemplo, cualquier disciplina que intenta predecir el comportamiento humano, como la psicología, normalmente tiene valores del R-cuadrado inferiores al 50%. Los seres humanos son simplemente más difíciles de predecir que, por ejemplo, los procesos físicos.
Además, si el valor del R-cuadrado es bajo pero se tiene predictores estadísticamente significativos, aún se puede obtener conclusiones importantes acerca de la asociación entre los cambios en los valores de los predictores y los cambios en el valor de respuesta. Independientemente del R-cuadrado, los coeficientes significativos aún representan el cambio medio en la respuesta para una unidad de cambio en el predictor mientras se mantienen constantes los otros predictores del modelo. Obviamente, este tipo de información puede ser muy valiosa.
Un R-cuadrado bajo es más problemático cuando se desea crear predicciones que sean razonablemente precisas (tener un intervalo de predicción lo suficientemente pequeño). ¿Qué tan alto debe ser el R-cuadrado para la predicción? Bueno, eso depende de los requisitos en cuanto a la anchura del intervalo de predicción y de cuánta variabilidad esté presente en los datos. Aunque se requiere un R-cuadrado alto para tener predicciones precisas, eso no es suficiente por sí solo, como veremos.
¿Son inherentemente Buenos los Valores Altos del R-cuadrado?
¡No! Un R-cuadrado alto no necesariamente indica que el modelo tiene un buen ajuste. Eso podría sorprendernos, pero examinemos la gráfica de línea ajustada y la gráfica de residuos de abajo. La gráfica de línea ajustada muestra la relación entre la movilidad de electrones del semiconductor y el logaritmo natural de la densidad correspondiente a los datos experimentales reales.
La gráfica de línea ajustada muestra que estos datos siguen una función bastante estrecha y el R-cuadrado es 98,5%, lo que suena genial. Sin embargo, si observamos más de cerca, veremos cómo la línea de regresión predice sistemáticamente datos demasiado altos o demasiado bajos (sesgo) en diferentes puntos a lo largo de la curva. También se pueden ver patrones en la gráfica de residuos vs. ajustes, en lugar de la aleatoriedad que se desea ver. Esto indica un mal ajuste, y es un recordatorio de por qué siempre se recomienda revisar las gráficas de residuos.
Este ejemplo proviene de mi publicación acerca de cómo elegir entre regresión lineal y no lineal. En este caso, la respuesta es utilizar la regresión no lineal, porque los modelos lineales no pueden ajustarse a la curva específica que siguen estos datos.
Sin embargo, sesgos similares pueden ocurrir cuando faltan predictores, términos polinómicos y términos de interacción importantes en el modelo lineal. Los especialistas en estadística se refieren a esto como “sesgo de especificación” y es causado por un modelo subespecificado. Para este tipo de sesgo, se pueden corregir los residuos al agregar los términos adecuados al modelo.
Para obtener más información sobre por qué un R-cuadrado alto no siempre es algo bueno, lea mi publicación Cinco razones por las que su R-cuadrado puede ser demasiado alto.
Reflexiones finales sobre el R-cuadrado
El R-cuadrado es una medida práctica y aparentemente intuitiva de qué tan bien se ajusta un modelo lineal a un conjunto de observaciones. Sin embargo, como pudimos ver, el R-cuadrado no nos cuenta toda la historia. Los valores del R-cuadrado se deben evaluar junto con las gráficas de residuos, otras estadísticas del modelo y el conocimiento de la materia para poder completar el cuadro (perdón por el juego de palabras).
Aunque el R-cuadrado provee una estimación de la fuerza de la relación entre el modelo y la variable de respuesta, no proporciona una prueba de hipótesis formal para esta relación. La prueba F de la significancia general determina si esta relación es estadísticamente significativa.
En mi próximo blog, continuaremos con el tema de que el R-cuadrado por sí solo es incompleto y veremos otros dos tipos de R-cuadrado: el R-cuadrado ajustado y el R-cuadrado de predicción. Estas dos medidas superan problemas específicos con el fin de proporcionar información adicional que permite evaluar el poder explicativo del modelo de regresión.
Para más información sobre el R-cuadrado, conozcan la respuesta a esta pregunta eterna: ¿Qué tan alto debe ser el R-cuadrado?
¡Si están aprendiendo sobre la regresión, pueden leer mi tutorial sobre regresión!/p>