Pour estimer le niveau de capabilité d’un procédé, les limites de spécification d'un produit sont comparées aux extrémités de la distribution des caractéristiques mesurées. La normalité des données est donc une condition essentielle.
Les diagrammes de probabilité sont très utiles pour vérifier la normalité des observations.
Cet article vous explique comment procéder lorsque vous observez un regroupement des données sur un diagramme de probabilité.
En effet, en pratique, on observe assez souvent des diagrammes de probabilité comme celui affiché ci-dessous.
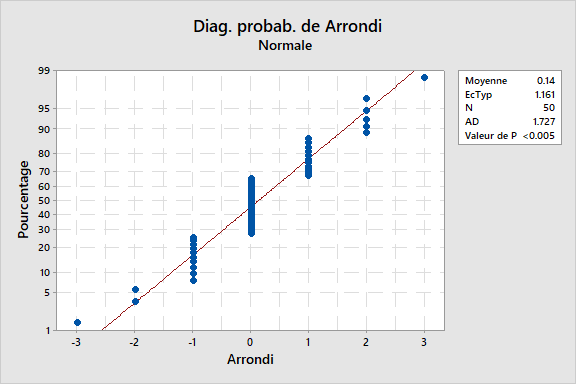
C’est une situation qui peut sembler assez déroutante. La ligne rouge du diagramme de probabilité, passe au milieu des données, indiquant un bon ajustement à la loi normale, et pourtant on observe des groupes de points superposés, agglomérés avec des valeurs mesurées strictement équivalentes, comme s’il s’agissait de données discrètes. La variable est continue en réalité mais sa véritable valeur n’est pas connue avec précision et les regroupements de données sur le diagramme de probabilité sont dus uniquement à une imprécision du système de mesure, comme si les données avaient été arrondies à l’entier inférieur.
Dans ce type de configuration, le test de normalité d’Anderson-Darling (AD) aboutit très souvent à un rejet de l’hypothèse de normalité à cause de l’approximation de la mesure, p inférieur à 0,05, alors qu’en réalité les données suivent bien une loi normale, les arrondis sont tout simplement liés au système de mesure.
Le test de normalité de Ryan-Joiner (RJ) est beaucoup moins sensible à ce phénomène.
Ainsi, dans ce même exemple (voir le graphique ci-dessous), la valeur de p pour le test de normalité avec la méthode de Ryan-Joiner est supérieure à 0,10 (donc dans ce contexte on ne peut raisonnablement plus rejeter l’hypothèse de normalité).
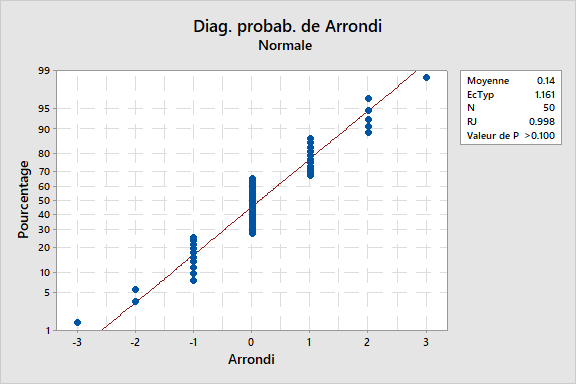
A quoi pourrait ressembler le diagramme de probabilité si nous pouvions reconstituer les vraies valeurs de la variable continue ?
Les données sont devenues discrètes à cause de l’inexactitude des données collectées par le système de mesure, mais nous pourrions faire en sorte de générer un peu de variabilité supplémentaire pour que la distribution redevienne continue.
Nous utiliserons une simulation à partir d’une loi uniforme, pour reconstituer la distribution des vraies valeurs comme si ces valeurs mesurées n’avaient pas été tronquées par intervalle. Il suffit d’ajouter du « bruit », c’est-à-dire des variations aléatoires, aux données arrondies/discrètes pour retrouver une distribution continue comme sur le diagramme de probabilité ci-dessous.
Dans cet exemple, les mesures ont été arrondies à l’entier le plus proche. Une valeur aléatoire de -0,5 à +0,5 (du bruit) a été ajoutée à chaque observation pour obtenir une mesure continue simulée.
Les instructions à suivre sont précisées ci-dessous :
Stockez les valeurs de bruit simulées de -0,5 à +0,5 dans une colonne de la feuille de travail en sélectionnant le sous-menu Calc > Données aléatoires > Loi Uniforme, dans le logiciel Minitab.
Utilisez le sous-menu > Calc > Calculatrice pour ajouter la colonne de bruit à la colonne de données d'origine. Pour un petit échantillon de données, il sera sans doute nécessaire de répéter la procédure plusieurs fois.
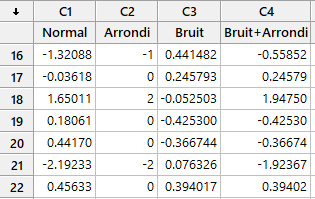
Enfin, créez un diagramme de probabilité (normal) à l’aide du sous-menu > Stat > Statistiques de base > Test de normalité.
Le graphique affiché ci-dessous suggère que la distribution normale est devenue un bon modèle pour décrire les observations. C'est un diagramme de probabilité avec mesures simulées.
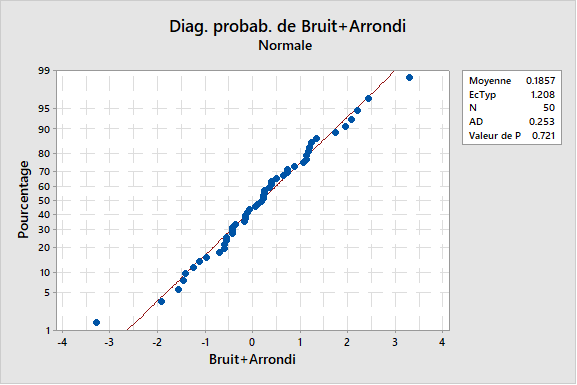
Conclusion
Le regroupement des données sur un diagramme de probabilité est un problème très fréquent en pratique et assez déroutant. La distribution des valeurs mesurées devient discrète et ne suit plus aucune loi continue. Il existe cependant des solutions pour cela, disponibles dans Minitab, comme celle proposée dans cet article.
Une alternative, un peu plus complexe, pour gérer ces valeurs tronquées par intervalles consisterait à exploiter par le menu Fiabilité / Survie de Minitab, plus précisément dans la partie > Analyse de répartition (troncature arbitraire), le sous-menu > Analyse de répartition paramétrique, pour prendre en compte la troncature par intervalle des données.
Le cours Analyse de données non normales avec le logiciel de statistiques Minitab, vous apprendra à détecter la non normalité, à choisir la distribution ou la transformation adaptée à votre analyse et à vérifier l'impact d'une résolution de mesures et d'un effectif d'échantillon insuffisants sur les tests de normalité. Contactez notre équipe Formation pour programmer ce cours en intra-entreprise ou en inter-entreprises.



