 *Alguns dos links relacionados podem conter informações em outros idiomas
*Alguns dos links relacionados podem conter informações em outros idiomas
Muitas vezes pensamos em uma relação entre duas variáveis como uma linha reta. Ou seja, se você aumentar a preditora em 1 unidade, a resposta sempre aumentará em X unidades. Entretanto, nem todos os dados têm uma relação linear e seu modelo deve se ajustar às curvas presentes nos dados.
Este gráfico de linha ajustada mostra a bobagem de usar uma linha para ajustar uma relação curvilínea!
Como você ajusta uma curva aos seus dados? Felizmente, o software estatístico Minitab inclui uma variedade de métodos de ajuste de curva, tanto na regressão linear como na regressão não linear.
Para comparar esses métodos, vou ajustar os modelos a essa curva no gráfico de linha ajustada. Para nossos propósitos, vamos supor que esses dados vêm de um processo físico de baixo ruído que tem uma função curva. Queremos prever com precisão a saída, dada a entrada. Aqui estão os dados para você tentar sozinho!
Curvas de ajuste com termos polinomiais em regressão linear
A maneira mais comum de ajustar curvas aos dados usando a regressão linear é incluir termos polinomiais, como preditores quadrados ou cubos .
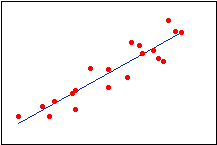
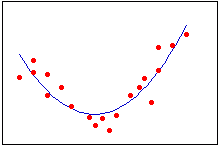
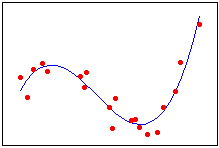
Normalmente, você escolhe a ordem do modelo pelo número de inflexões que você precisa em sua linha. Cada aumento no expoente produz mais uma inflexão na linha curva. É muito raro usar mais do que um termo cúbico.
| Linear | Quadrático | Cúbico |
|---|---|---|
 |
 |
 |
O gráfico dos nossos dados parece ter uma curvatura, então vamos tentar ajustar um modelo linear quadrático usando Estat> Gráfico de linha ajustada.

Ao mesmo tempo que o R-quadrado é alto, o gráfico de linha ajustada mostra que a linha de regressão sistematicamente prevê acima e abaixo dos dados, em diferentes pontos da curva. Isto mostra que nem sempre é possível confiar em um R-quadrado elevado.
Vamos ver se podemos fazer melhor.
Ajuste de curvas com termos recíprocos em regressão linear
Se os dados da resposta descerem até um piso, ou subirem até um teto à medida que a entrada aumenta (por exemplo, se aproxima de uma assíntota), você pode ajustar esse tipo de curva na regressão linear incluindo a recíproca (1/X) de uma ou mais variáveis preditoras no modelo. De forma mais geral, você deseja usar esta forma quando o tamanho do efeito de uma variável preditora diminui à medida que seu valor aumenta.
Como a inclinação é uma função de 1/X, a inclinação fica mais plana à medida que X aumenta. Para este tipo de modelo, X nunca pode ser igual a 0 porque você não pode dividir por zero.
Olhando para os nossos dados, eles parecem estar se achatando e se aproximando de uma assíntota em torno de 20.
Eu usei o Calc> Calculadora no Minitab para criar uma coluna 1/Entrada (InvEntrada). Vamos ver como isso funciona! Eu o encaixo com um modelo linear (parte superior) e quadrático (parte inferior).


Para este exemplo em particular, o modelo recíproco quadrático ajusta muito melhor os dados. Os gráficos da linha ajustada alteram o eixo x para 1/Entrada, por isso é difícil ver a curvatura natural dos dados.
No gráfico de dispersão abaixo, usei as equações para plotar pontos ajustados para ambos os modelos na escala natural. Os pontos de dados em cor verde caem claramente mais perto da linha quadrática.

Em comparação com o modelo quadrático, o modelo recíproco com o termo quadrático tem um valor S mais baixo (bom), R-quadrado maior (bom) e não mostra as previsões com viés. Até agora este é o nosso melhor modelo.
Transformar variáveis com funções de log na regressão linear
Uma transformação logarítmica é um método relativamente comum que permite que a regressão linear execute ajustes de curva que, caso contrário, só seriam possíveis na regressão não linear.
Por exemplo, a função não linear:
Y=eB0X1B1X2B2
pode ser expressa na forma linear de:
Ln Y = B0 + B1lnX1 + B2lnX2
Você pode pegar o log em ambos os lados da equação, como acima, que é chamado de forma duplo-log. Ou você pode pegar o log de apenas um lado, conhecido como o forma semi-log. Se você pegar os logs no lado da preditora, pode ser para todos ou apenas alguns das preditoras.
As formas funcionais de log podem ser bastante poderosas, mas há muitas combinações para entrar em detalhes nessa visão geral. A escolha de duplo-log versus semi-log (para a resposta ou preditoras) depende das especificidades de seus dados e do conhecimento da área. Em outras palavras: se você seguir esse caminho, precisará fazer algumas pesquisas.
Vamos voltar ao nosso exemplo. Para dados em que a curva se achata à medida que a preditora aumenta, um modelo semi-log da(s) preditor(as) relevante(s) pode ser ajustado. Vamos tentar!
O gráfico de linha ajustada do Minitab tem a opção de fazer a transformação log de um ou ambos os lados do modelo. Então eu transformei apenas a variável preditora no gráfico de linha ajustada abaixo.

Visualmente, podemos ver que o modelo semi-log sistematicamente prevê para cima e para baixo os dados em diferentes pontos da curva, assim como o modelo quadrático. Os valores S e de R-quadrado também são virtualmente idênticos àquele modelo.
Até agora, o modelo linear com os termos recíprocos ainda fornece o melhor ajuste para nossos dados curvos.
Ajustar curvas com regressão não linear
A regressão não linear pode ser uma alternativa poderosa à regressão linear, pois fornece a funcionalidade do ajuste de curva mais flexível. O truque é encontrar a função não linear que melhor se adapte à curva específica de seus dados. Felizmente, o Minitab fornece ferramentas para tornar isso mais fácil.
Na caixa de diálogo Regressão não linear ( Estat > Regressão > Regressão não linear), insira Saída para Resposta. Em seguida, clique em Usar catálogo para escolher entre as funções não lineares fornecidas pela Minitab.
Sabemos que nossos dados se aproximam de uma assíntota, então podemos clicar nas duas funções de Regressão assintótica. A versão côncava corresponde aos nossos dados mais de perto. Escolha essa função e clique em OK.

Em seguida, o Minitab exibe uma caixa de diálogo na qual escolhemos nossa preditora.

Digite Entrada, clique em OK e estamos de volta à caixa de diálogo principal.
Se clicarmos em OK na caixa de diálogo principal, o Minitab exibirá a seguinte caixa de diálogo:

Ao contrário da regressão linear, a regressão não linear usa um algoritmo para encontrar o melhor ajuste passo a passo. Precisamos dar os valores iniciais para cada parâmetro na função. Ai caramba, não tenho ideia! Felizmente, o Minitab facilita isso.

Vamos olhar novamente a função que escolhemos. A imagem torna isto mais fácil!
Observe que Theta1 é a assíntota ou o teto que nossos dados se aproximam. De acordo com o gráfico de dispersão inicial, é cerca de 20 para os nossos dados. Para um caso como o nosso, onde a resposta se aproxima de um teto à medida que a preditora aumenta, Theta2 > 0 e Theta3 > 0.
Consequentemente, vou inserir o seguinte na caixa de diálogo:
- Theta1: 20
- Theta2: 1
- Theta3: 1
Depois de inserirmos esses valores, voltamos à caixa de diálogo principal, clicamos em OK e voilà!


É impossível calcular o R-quadrado para a regressão não-linear, mas o valor S para o modelo não-linear (0.179746) é quase tão pequeno quanto o do modelo recíproco (0.34828). Você quer um S pequeno porque significa que os pontos de dados caem mais perto da linha curva. O modelo não linear também não tem um viés sistemático.
Comparando a efetividade de ajuste da curva dos diferentes modelos
| Modelo |
R-quadrado |
S |
Ajustes viesados |
| Recíproco - Quadrático |
99.9 |
0.134828 |
Não |
| Não linear |
N/D |
0.179746 |
Não |
| Quadrático |
99.0 |
0.518387 |
Sim |
| Semi-Log |
98.6 |
0.565293 |
Sim |
| Recíproca - Linear |
90.4 |
1.49655 |
Sim |
| Linear |
84.0 |
1.93253 |
Sim |
O modelo linear com o termo recíproco quadrático e o modelo não linear são melhores que os outros modelos. Esses dois modelos superiores produzem previsões igualmente boas para a relação curvilínea. Entretanto, o modelo de regressão linear com os termos recíprocos também produz valores-p para as preditoras (todas significativas) e um R-quadrado (99.9%), nenhum dos quais você pode obter para um modelo de regressão não-linear.
Para este exemplo, essas estatísticas extras podem ser úteis para relatórios, mesmo que os resultados não lineares sejam igualmente válidos. No entanto, nos casos em que o modelo não linear fornece o melhor ajuste, você deve escolher o melhor ajuste.
Qual é a diferença entre as equações de regressão linear e não linear?
Considerações finais
Se você tem uma curva difícil para ajustar, encontrar o modelo correto pode parecer uma tarefa difícil. Mas depois de todo o esforço para coletar os dados, vale a pena o esforço para encontrar o melhor ajuste possível.
Ao especificar qualquer modelo, você deve deixar a teoria e o conhecimento da área de assunto guiá-lo. Algumas áreas têm práticas e funções padrão para modelar os dados.
Ao mesmo tempo que você quer um bom ajuste, você não quer inflar artificialmente o R-quadrado com um modelo excessivamente complicado. Esteja ciente que:
- O R-quadrado pode ser enganoso
- Modelos excessivamente complicados podem produzir resultados enganosos
- Verifique os gráficos de resíduos para evitar resultados enganosos (eu não os mostrei neste post, mas eu os chequei!)
Se você está aprendendo sobre regressão, leia meu tutorial sobre regressão!



