*Alguns dos links relacionados podem conter informações em outros idiomas
Depois de ajustar um modelo linear usando análise de regressão, ANOVA ou DOE (Planejamento de Experimentos), você precisa determinar quão bem o modelo se ajusta aos dados. Para ajudá-lo, o Minitab tem várias estatísticas de teste de qualidade de ajuste. Neste post nós vamos explorar a estatística R-quadrado (R2), algumas de suas limitações e descobrir algumas surpresas ao longo do caminho. Por exemplo: valores baixos de R-quadrado nem sempre são ruins e valores altos de R-quadrado nem sempre são bons!
O que é o Teste de qualidade de ajuste para um Modelo linear??
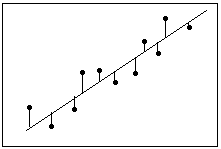Definição: Resíduos = Valor observado - Valor ajustadoA regressão linear calcula uma equação que minimiza a distância entre a linha ajustada e todos os pontos de dados. Tecnicamente, a regressão por mínimos quadrados ordinários (MQO) minimiza a soma dos resíduos quadrados.
Em geral, um modelo ajusta bem os dados se as diferenças entre os valores observados e os valores previstos do modelo forem pequenos e não viesados.
Antes de olhar para as medidas estatísticas do teste de qualidade de ajuste, você deve verificar os gráficos de resíduos. Os gráficos de resíduos podem revelar padrões indesejados nos resíduos, que indicam resultados viesados de forma mais eficaz do que os números. Quando os gráficos de resíduos forem aceitos, você poderá confiar nos resultados numéricos e verificar as estatísticas de teste de qualidade de ajuste.
O que é o R-quadrado?
O R-quadrado é uma medida estatística de quão próximos os dados estão da linha de regressão ajustada. Ele também é conhecido como o coeficiente de determinação ou o coeficiente de determinação múltipla para a regressão múltipla.
A definição do R-quadrado é bastante simples: é a porcentagem da variação da variável resposta que é explicada por um modelo linear. Ou:
R-quadrado = Variação explicada/Variação total
O R-quadrado está sempre entre 0 e 100%:
- 0% indica que o modelo não explica nada da variabilidade dos dados de resposta ao redor de sua média.
- 100% indica que o modelo explica toda a variabilidade dos dados de resposta ao redor de sua média.
Em geral, quanto maior o R-quadrado, melhor o modelo se ajusta aos seus dados. No entanto, existem condições importantes para esta diretriz.
Representação gráfica do R-quadrado
Plotar os valores ajustados pelos valores observados ilustra graficamente valores diferentes de R-quadrado para os modelos de regressão.
O modelo de regressão à esquerda explica 38,0% da variância, enquanto o da direita explica 87,4%. Quanto mais variância for explicada pelo modelo de regressão, mais próximos os pontos de dados estarão em relação à linha de regressão ajustada. Teoricamente, se um modelo pudesse explicar 100% da variância, os valores ajustados seriam sempre iguais aos valores observados e, portanto, todos os pontos de dados cairiam na linha de regressão ajustada.
Principais limitações do R-quadrado
O R-quadrado não pode determinar se as estimativas e predições dos coeficientes são tendenciosas, e é por isso que você deve avaliar os gráficos de resíduos.
O R-quadrado não indica se um modelo de regressão é adequado. É possível ter um valor baixo de R-quadrado para um bom modelo ou um valor alto de R-quadrado para um modelo que não se encaixa nos dados!
O R-quadrado na saída é uma estimativa tendenciosa da população R-quadrada.
Valores baixos de R-quadrado são necessariamente ruins?
Não! Existem duas razões principais pelas quais pode ser muito bom ter valores baixos de R-quadrado.
Em algumas áreas, é totalmente esperado que seus valores de R-quadrado sejam baixos. Por exemplo, qualquer área que tente prever o comportamento humano (como a psicologia) normalmente tem valores de R-quadrado menores que 50%. Seres humanos são mais difíceis de prever do que, digamos, processos físicos.
Além disso, se seu valor de R-quadrado for baixo mas você tiver preditoras estatisticamente significativas, ainda poderá tirar conclusões importantes sobre como as alterações nos valores das variáveis preditoras estão associadas a alterações no valor da variável resposta. Independentemente do R-quadrado, os coeficientes significativos ainda representam a mudança média na resposta para uma unidade de mudança na preditora, mantendo as outras preditoras do modelo constantes. Obviamente, esse tipo de informação pode ser extremamente valiosa.
Um R-quadrado baixo é mais problemático quando você deseja produzir previsões que sejam razoavelmente precisas (que tenham um intervalo de predição que seja pequeno o suficiente). Quão alto o R-quadrado deve ser para predição? Bem, isso depende dos seus requisitos quanto à largura de um intervalo de predição e de quanta variabilidade está presente em seus dados. Enquanto um R-quadrado alto é necessário para predições precisas, não é suficiente por si só (como veremos).
Valores altos do R-quadrado são necessariamente bons?
Não! Um R-quadrado alto não indica necessariamente que o modelo tem um bom ajuste. Isso pode ser uma surpresa, mas olhe para o gráfico de linha ajustada e o gráfico de resíduos abaixo. O gráfico de linha ajustada exibe a relação entre a mobilidade eletrônica de semicondutores e o log natural da densidade, para dados experimentais reais.
O gráfico de linha ajustada mostra que esses dados seguem uma função bem ajustada e o R-quadrado é 98,5%, o que parece ótimo. No entanto, olhe mais de perto para ver como a linha de regressão sistematicamente prevê os dados para cima e para baixo (viés) em diferentes pontos ao longo da curva. Você também pode ver padrões no gráfico Resíduos versus valores ajustados, ao invés vez da aleatoriedade que deseja ver. Isso indica um ajuste ruim e serve como um lembrete de porque você deve sempre verificar os gráficos de resíduos.
Este exemplo vem do meu post sobre como escolher entre regressão linear e não linear. Nesse caso, a solução é usar a regressão não linear, pois os modelos lineares não conseguem um bom ajuste para a curva específica que esses dados seguem.
No entanto, vieses semelhantes podem ocorrer quando seu modelo linear está perdendo importantes variáveis preditoras, termos polinomiais e termos de interação. Os estatísticos chamam isso de viés de especificação e isso é causado por um modelo sub-especificado. Para esse tipo de viés, você pode corrigir os resíduos adicionando os termos adequados ao modelo.
Para obter mais informações sobre como um R-quadrado alto nem sempre é bom, leia o meu post Cinco razões pelas quais o R-quadrado pode ser muito alto.
Considerações finais sobre o R-quadrado
O R-quadrado é uma medida prática e aparentemente intuitiva de quão bem seu modelo linear se ajusta a um conjunto de observações. No entanto, como vimos, o R-quadrado não conta toda a história. Você deve avaliar os valores do R-quadrado em conjunto com os gráficos de resíduos, as outras estatísticas do modelo e o conhecimento da área para arredondar a imagem (com o perdão do trocadilho).
Embora o R-quadrado forneça uma estimativa da força do relacionamento entre seu modelo e a variável resposta, ele não fornece um teste de hipóteses formal para esse relacionamento. O teste F para significância global determina se esta relação é estatisticamente significativa.
No meu próximo blog continuaremos com o tema onde o R-quadrado per se é incompleto, e olharemos para outros dois tipos de R-quadrado: O R-quadrado ajustado e o R-quadrado predito. Essas duas medidas superam problemas específicos a fim de fornecer informações adicionais através das quais você pode avaliar o poder explicativo do seu modelo de regressão.
Para saber mais sobre o R-quadrado, aprenda a resposta para esta eterna pergunta: Quão alto deve ser o R-quadrado?
Se você está aprendendo sobre regressão, leia meu tutorial sobre regressão!