Suppose that on your way to a summer holiday resort (a very distant place), your car breaks down. You might just call the roadside assistance and wait for your car to be towed to a repair shop. But suppose that you think you are smarter than that, and you would like to solve the issue by yourself—or at least evaluate the repair cost. Vehicle breakdowns can occur for a large number of reasons.
Intuitively, when facing a complex problem, we tend to test different solutions as soon as they come to our mind. When we understand that one solution will not work, we will then look for the next potential solution in order to test it and so forth. This is what we will call the one-factor-at-a-time approach, which is very intuitive, and very popular in companies across the globe when it comes to fixing complex quality issues. Parameters are changed and tested one at a time until the problem is fixed. It looks a little something like this: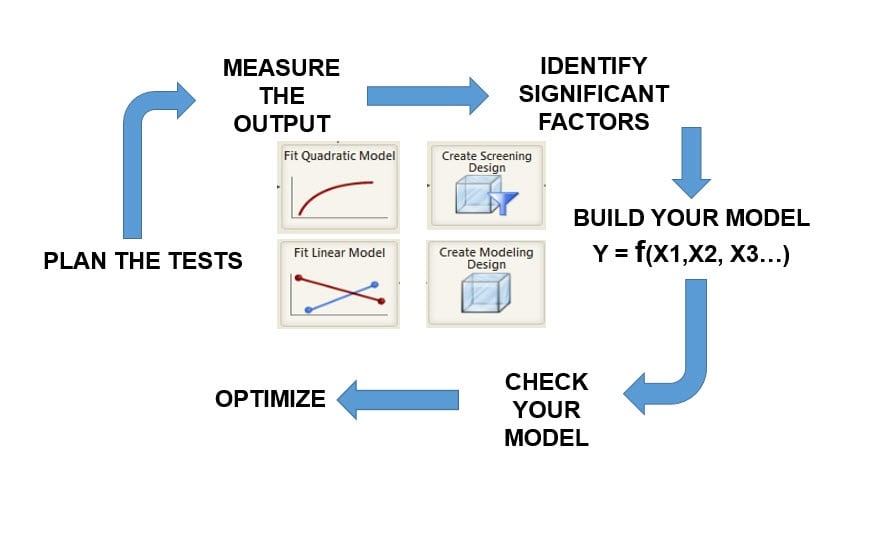
In a design of experiments though, the approach is completely different—all parameters settings are changed together, simultaneously, according to a DOE array like the one below:
Table 1 – A DOE array in Minitab to specify all factor settings for each experimental run.
Multiple Benefits of Experimental Design
So why is it better to perform a Design of Experiments (DOE) rather than change One Factor at a Time, then? And what are the multiple benefits of an experimental design?
1) Effect estimates precision (primarily)
In a two-level experimental design, for every parameter setting, we can calculate an average from the tests that have been performed (an average for the low setting of a factor and an average for the high setting). The effect of a two-level factor is the difference between the average for the low setting and the average for the high setting. Therefore, in a DOE, we actually compare averages to other averages rather than individual values to other individual values (as in a One-Factor-At-a-Time experiment). This allows us to reach a much greater level of accuracy in the effect estimates for a given number of trials, and thus the influential factors are much more likely to emerge from the environmental noise (which represents the experimental error, the surrounding variability etc…).
Since experimental designs provide much more accurate estimates, this may also be helpful to compensate for a lack of accuracy in the measurement system, for example.
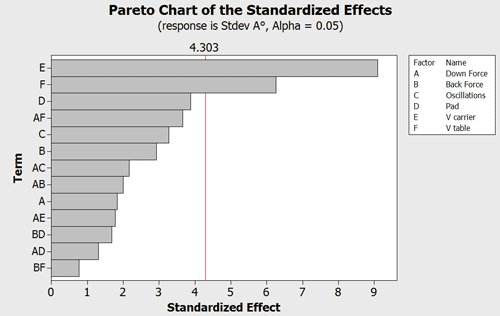
Graph 1 – A Pareto chart in Minitab to identify the effects that are significant.
2) Factor interactions
The possibility to estimate interactions between factors is another major strength of an experimental design. The effect of factor A, for example, may be much larger when factor B is set at a specific level, leading to an interaction (coupling effects, synergies or antagonisms between factors). A very well known example of an interaction that comes to my mind is the interaction between alcohol and sleeping pills on the braking distance of a car.
Suppose that a motorist decided to test the effect of alcohol, and that as a consequence of drinking a large quantity of alcohol, his braking distance (and time to react) increased significantly. Suppose that the same motorist also took (many) sleeping pills. Sleeping pills and alcohol will interact leading to an effect that is much larger than the simple addition of the sleeping pills effect plus the alcohol effect. Of course, changing one factor at a time will never allow you to identify interactions, but a DOE will.
3) Balance within the design (or design orthogonality)
In a standard experimental design, each level of each factor is associated as many times with each level of each one of the other factors, leading to a design with balanced combinations of levels. This enables one to estimate the effects of each factor independently from the effects of all other factors. The estimates are not biased by other effects from other factors.
This is important, since if rather than perform a balanced DOE, we consider observational data (from a database for example), and, by chance, a parameter changes at the same time as another parameter, it will become very difficult to separate these effects (that might be the case when a regression analysis is performed on historical data). On the other hand, a DOE allows one to truly estimate the specific effect of each factor without bias.
To conclude, the One-Factor-at-a-Time approach, although very popular and intuitive, is not an efficient way to solve issues unless you are dealing with a very simple problem. It is always better to perform a design of experiments (DOE) rather than change parameters One Factor at a Time.



