工程から観察データを収集していくと、有意義な洞察を得ることのできる新しいツールが必要になる場合があります。工程を分析、改善、管理するために、従来の統計ツールに加えて、機械学習の技術を追加することができます。二値ロジスティック回帰と分類木(CART®)の例を見ていきましょう。
編集者のメモ:Salford Predictive ModelerでCARTを表示するこの投稿の以前のバージョンは、2018年3月に公開されました。最新バージョンのMinitabでCARTを表示するように更新しました。
パルプ漂白工程での過度な変動の根本原因の発見
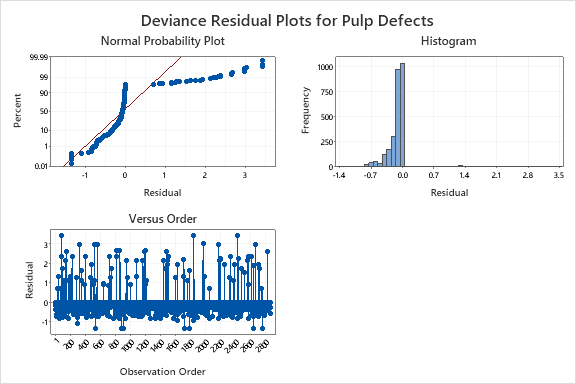
この例では、製品の2.9%が欠陥品です。この工程の不合格品の根本原因を見ていくために、Minitabの二値ロジスティック回帰から始めることができます。ここでの応答変数とは、観測値が欠陥か否かです。残念ながら、このデータの場合、残差プロットの乱れたパターンが二値ロジスティック回帰モデルが不十分かもしれないことを示しています。
CARTのアプローチ
CARTは、予測因子(X)設定に基づいて応答(Y)変数を分割する、一連の「はい」または「いいえ」ルールを作成することによって機能する決定木アルゴリズムです。MinitabでCART機能を使用し、予測変数の1つ、放電pHが欠陥の大因子であることがわかります。

放電pHが7.739以下の場合、欠陥の推定確率は比較的高くなります(17.7%)。放電pHが7.739より高い場合、欠陥の発生はわずかです。
詳細:

下のMinitabのグラフで、なぜルールが機能するのかが説明されています。CARTモデルで、応答 = 合格グループと応答 = 不合格グループを最適に分離する変数と設定を見つけることができます。ここでは、その変数と設定は放電pH 7.739です。

CART木を成長させ続ければ、この工程の欠陥につながる設定の組み合わせをもっとたくさん見つけることができます。問題をいくつかの重要なXに絞り込んだら、欠陥の発生確率を減らすような管理を行うことができます。この場合、完全なCART分類モデルで、下のグラフのように、不均衡な欠陥数につながる放電pHと生産率のいくつかの特定の組み合わせを識別することができるのです。

ご自分の目で確かめてみませんか?





